 Polynômes du second degré
Polynômes du second degré
Exercice 12
Certaines questions de cet exercice portent sur la PARTIE 2 du cours sur les trinômes.On considère la courbe $P$ tracée dans un repère orthonormé.
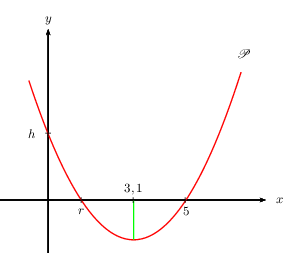
Cette courbe représente la fonction $f$ définie pour tout $x$ de $ℝ$ par
$f(x)=ax^2+bx+c$ (où $a$, $b$ et $c$ sont des réels avec $a$ non nul).
- Quelle est la nature de la courbe $P$?
- Est-il exact que $a$<$0$?
- Donner l'équation réduite de l'axe de symétrie de $P$.
- Que vaut la somme des 2 racines de $f$?
- Déterminer la valeur de $r$.
- On pose $\Δ=b^2-4ac$. Est-il exact que $\Δ≤0$?
- Que vaut le produit des 2 racines de $f$?
- On suppose que $h=2,4$. Déterminer la valeur de $c$.
- En déduire les valeurs de $a$ et $b$.
Corrigé

- Pour tout $x$ de $ℝ$, $f(x)=ax^2+bx+c$ (où $a$, $b$ et $c$ sont des réels avec $a$ non nul).
$f$ est donc un trinôme du second degré. Or $P$ est sa courbe représentative dans un repère orthonormé. Donc la courbe $P$ est une parabole. - Le trinôme $f$ est d'abord décroissant, puis il est croissant. Par conséquent: $a$>$0$.
Donc l'affirmation $a$<$0$ est fausse. - L'axe de symétrie de $P$ a pour équation $x=3,1$.
- La somme des 2 racines de $f$ vaut ${-b}/{a}$.
Or l'axe de symétrie de de $P$ a pour équation $x={-b}/{2a}$.
Par conséquent, d'après le 3., on obtient: ${-b}/{2a}=3,1$, et par là, la somme des 2 racines de $f$ vaut $6,2$ - $r$ et 5 sont les 2 racines de $f$. Donc on obtient: $r+5=6,2$
Et par là: $r=1,2$. - $\Δ=b^2-4ac$ est le discriminant du trinôme $f$, qui admet exactement 2 racines. Donc $\Δ$>$0$.
Donc l'affirmation $\Δ≤0$ est fausse. - Le produit des 2 racines de $f$ vaut $1,2×5=$$6$.
- On suppose que $h=2,4$. Or $h=f(0)=c$. Donc $c=2,4$.
A retenir: l'ordonnée à l'origine d'une parabole représentant un trinôme donne la valeur de $c$ - Le produit des 2 racines de $f$ vaut ${c}/{a}$.
Donc: ${2,4}/{a}=6$.
Et par là: $a=0,4$.
La somme des 2 racines de $f$ vaut ${-b}/{a}$.
Donc: ${-b}/{0,4}=1,2+5$.
Et par là: $b=2,48$
Autre méthode pour déterminer $b$.
On développe la forme factorisée de $f$.
On a: $(x)=0,4(x-1,2)(x-5)=0,4(x^2-6,2x+6)=0,4x^2-2,48x+2,4$
On retrouve le fait que $b=-2,48$