 Polynômes du second degré
Polynômes du second degré
Exercice 7
On considère le rectangle ABCD, dans lequel on a inscrit le quadrilatère EFGH.
On suppose que: $AB=4$ , $BC=2$ et $AE=BF=CG=DH=x$.
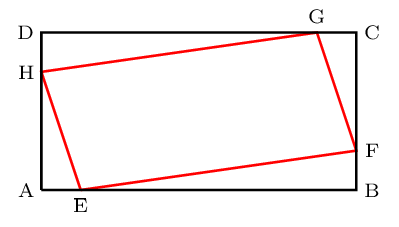
- Exprimer l'aire du triangle AEH en fonction de $x$.
- Montrer que l'aire du quadrilatère EFGH est $f(x)=2(x^2-3x+4)$.
- Déterminer la forme canonique de $x^2-3x+4$ par la méthode de complétion au carré.
En déduire l'écriture de $f$ sous forme canonique. - Déterminer alors la valeur de $x$ pour laquelle l'aire $f(x)$ est minimale.
Corrigé
- Il est clair que le triangle AEH est rectangle en A.
Son aire est donc égale à:
${AE×AH}/{2}={x×(2-x)}/{2}$. - De même, on obtient l'aire du BFE qui vaut:
${BF×BE}/{2}={x×(4-x)}/{2}$.
Le triangle CGF a clairement même aire que le triangle AEH, et le triangle DHG a clairement même aire que le triangle BFE.
Par ailleurs, l'aire du quadrilatère EFGH est égale à l'aire du rectangle ABCD privé des 4 triangles précédents.
On obtient donc: $f(x)=AB×BC-2×{x×(2-x)}/{2}-2×{x×(4-x)}/{2}$
Soit: $f(x)=4×2-x×(2-x)-x×(4-x)$
Soit: $f(x)=8-2x+x^2-4x+x^2$
Soit: $f(x)=2x^2-6x+8$
Soit: $f(x)=2(x^2-3x+4)$ - $f$ est un trinôme du second degré dont on a factorisé le coefficient dominant.
Déterminons sa forme canonique par la méthode de complétion du carré.
On a: $x^2-3x+4=x^2-2×x×1,5+1,5^2-1,5^2+4$
Soit: $x^2-3x+4=(x-1,5)^2-2,25+4$
Soit: $x^2-3x+4=(x-1,5)^2+1,75$
Et par là: $f(x)=2((x-1,5)^2+1,75)$
Soit: $f(x)=2(x-1,5)^2+3,5$ - On note tout d'abord que $f(1,5)=3,5$.
Or, comme $(x-1,5)^2$ est un carré, on a:
$(x-1,5)^2≥0$, et donc: $2(x-1,5)^2+3,5≥2×0+3,5$
Et par là: $f(x)≥f(1,5)$, et c'est vrai pour tout $x$.
Donc l'aire $f(x)$ est minimale pour $x=1,5$.