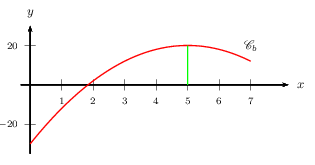
Polynômes du second degré
Polynômes du second degré
Exercice 8
Une entreprise fabrique et vend $x$ tonnes d'un certain produit P.
L'entreprise a une capacité de production maximale de 7 tonnes.
Soit $f(x)$ le coût de fabrication (en millions d'euros) de $x$ tonnes du produit P.
Soit $g(x)$ les recettes (en millions d'euros) obtenues pour la vente de $x$ tonnes du produit P.
On suppose que l'entreprise vend tout ce qu'elle fabrique.
Soit $b(x)$ le bénéfice (en millions d'euros) réalisé lorsque l'entreprise a vendu les $x$ tonnes qu'elle a fabriquées.
PARTIE A
- Les fonctions $f$ et $g$ sont représentées ci-dessous.
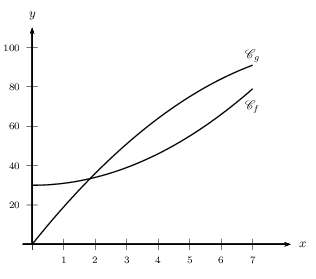
Déterminer graphiquement quelle production $x_{nul}$ assure un bénéfice nul à l'entreprise. On en donnera une valeur approchée à l'unité près. - Déterminer graphiquement quelles productions assurent un bénéfice strictement positif à l'entreprise.
- Déterminer graphiquement quelle production $x_M$ assure le bénéfice maximal. On en donnera une valeur approchée à l'unité près.
PARTIE B
Nous admettons désormais que $f(x)=x^2+30$ et $g(x)=-x^2+20x$.
Retouver les trois résultats obtenus dans la partie A par des considérations algébriques (toute justification graphique est ici interdite).
Cette fois-ci, la valeur de $x_{nul}$ sera arrondie au millième. On donnera la valeur exacte de $x_M$.
Corrigé
PARTIE A
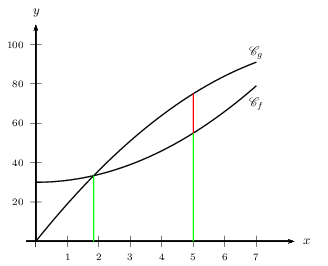
- Le bénéfice de l'entreprise est $b(x)=g(x)-f(x)$.
La production $x_{nul}$ vérifie $b(x_{nul})=0$, soit: $g(x_{nul})=f(x_{nul})$.
Graphiquement: $x_{nul}≈2$
Notons que la valeur exacte de $x_{nul}$ semble légèrement inférieure à 2. - Les productions $x$ qui assurent un bénéfice strictement positif à l'entreprise vérifient $b(x)>0$, ce qui est équivalent à: $g(x)>f(x)$.
Graphiquement: S$=]x_{nul};10]$
L'entreprise réalise un bénéfice si elle produit et vend au moins 2 tonnes de produit environ. - La production $x_M$ assure le bénéfice maximal est la valeur de $x$ telle que $b(x)$ est maximal, ce qui est équivalent à: $g(x)-f(x)$ est maximal.
On recherche la valeur de $x$ telle que l'écart $g(x)-f(x)$ soit le plus grand possible (en rouge sur le dessin).
Graphiquement: $x_M≈5$
Il semble même que l'on ait exactement $x_M=5$.
PARTIE B
Dans tout ce qui suit, les fonctions sont définies sur l'intervalle [0;7], car l'entreprise a une capacité de production maximale de 7 tonnes.
On a: $f(x)=x^2+30$ et $g(x)=-x^2+20x$.
On obtient alors: $b(x)=g(x)-f(x)=-x^2+20x-x^2-30=-2x^2+20x-30$
1. Recherche de $x_{nul}$.
On résout: $b(x)=0$, soit: $-2x^2+20x-30=0$
Le membre de gauche est un trinôme avec $a=-2$, $b=20$ et $c=-30$.
$Δ=b^2-4ac=20^2-4×(-2)×(-30)=160$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={-20-√{160}}/{-4}≈8,162$ et $x_2={-b+√Δ}/{2a}={-20+√{160}}/{-4}≈1,838$.
Seule la racine comprise entre 0 et 7 est valide.
Donc $x_{nul}≈1,838$
Une production d'environ 1,838 tonnes assure un bénéfice nul.
2. Recherche des productions assurant un bénéfice strictement positif à l'entreprise.
On résout: $b(x)>0$, soit: $-2x^2+20x-30>0$
Le membre de gauche est un trinôme ayant 2 racines $x_1≈8,162$ et $x_{nul}≈1,838$.
Sa forme factorisée est $-2(x-x_1)(x-x_{nul})$.
D'où les tableaux suivants:
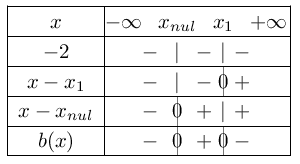
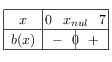
Donc S$=]x_{nul};10]$ avec $x_{nul}≈1,838$
L'entreprise doit produire (et vendre) plus de 1,838 tonnes (environ) pour avoir un bénéfice strictement positif.
3. Recherche de $x_M$.
La production $x_M$ assure le bénéfice maximal est la valeur de $x$ telle que $b(x)$ est maximal.
$b(x)$ est un trinôme avec $a=-2$, $b=20$ et $c=-30$.
Déterminons sa forme canonique par la méthode de complétion au carré.
Constatons tout d'abord que $b(x)=-2(x^2-10x+15)$
On a: $x^2-10x+15=x^2-2×x×5+5^2-5^2+15$
Soit: $x^2-10x+15=(x-5)^2-25+15$
Soit: $x^2-10x+15=(x-5)^2-10$
Et par là: $b(x)=-2((x-5)^2-10)$
D'où la forme canonique: $b(x)=-2(x-5)^2+20$
Montrons que le maximum de $b$ est atteint en 5.
On note tout d'abord que $b(5)=20$.
Or, comme $(x-5)^2$ est un carré, on a:
$(x-5)^2≥0$, et donc: $-2(x-1,5)^2+20≤-2×0+20$
Et par là: $b(x)≤b(5)$, et c'est vrai pour tout $x$.
Donc $x_M=5$.
L'entreprise doit produire (et vendre) 5 tonnes pour avoir un bénéfice maximal.
Notons que l'on peut retrouver facilement toutes ces informations en représentant graphiquement $b$.