Variations
Exercice 1
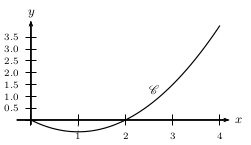
$f$ est définie sur $[0;4]$.
Elle est représentée par $\C$.
Résoudre graphiquement
$f(x)=0$
$f(x)≥0$
$f\,'(x)=0$
$f\,'(x)≥0$
Corrigé
$f(x)=0⇔x=0$ ou $x=2$. Donc $\S=\{0;2\}$.
$f(x)≥0⇔x=0$ ou $2≤x≤4$. Donc $\S==\{0\} ∪ [2;4]$.
$f\,'(x)=0⇔x=1$ (la tangente y est "horizontale"). Donc $\S=\{1\}$.
$f\,'(x)≥0⇔1≤x≤4$ (la courbe $\C$ y est croissante). Donc $\S=[1;4]$.