 Variations
Variations
Exercice 3
Un architecte a construit un monument en forme de cône de révolution, de hauteur OS=30 mètres, dont le rayon de la base vaut OB=10 mètres.
L'intérieur de l'édifice est en forme de cylindre de révolution de hauteur $OO_2=AC=h$ (avec $h$ entre 0 et 30), dont le rayon de la base vaut $OA=r$ mètres (avec $r$ entre 0 et 10), et dont le volume V est le plus grand possible (le cylindre affleure le toît).
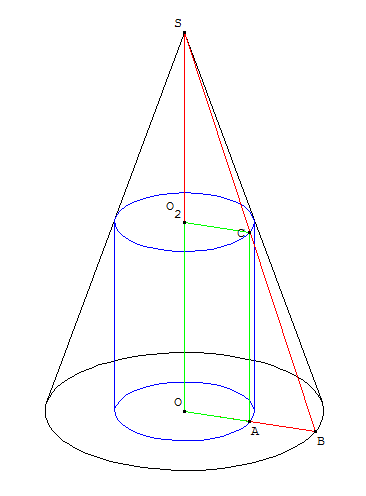
- Montrer que: $h=30-3r$.
- Prouver que $V=30πr^2-3πr^3$ pour $r$ entre 0 et 10.
- On pose $f(r)=30πr^2-3πr^3$.
Déterminer le tableau de variation de $f$. - Conclure.
Corrigé
- Il est clair que l'on peut appliquer le théorème de Thalès dans le triangle OBS, car les droites (AC) et (OS) sont évidemment parallèles.
On obtient en particulier: ${AC}/{OS}={BA}/{BO}$
Or: $AC=h$, $OS=30$, $BA=OB-OA=10-r$ et $BO=10$.
On obtient donc: ${h}/{30}={10-r}/{10}$
Et par là: $h=30×{10-r}/{10}=3(10-r)=30-3r$ - Le cylindre de révolution a pour volume: $V=πr^2h$
Donc on obtient: $V=πr^2(30-3r)$
Soit $V=30πr^2-3πr^3$ (et c'est vrai pour $r$ entre 0 et 10) - On pose $f(r)=30πr^2-3πr^3$.
Pour déterminer les variations de $f$, nous allons étudier le signe de $f'$
On obtient: $f'(r)=3πr(-3r+20)$
On a: $f'(r)=30π×2r-3π×3r^2=-9πr^2+60πr$
$f$ est un trinôme du second degré aisément factorisable!
On obtient: $f'(r)=3πr(-3r+20)$
On a là un produit.
$3πr$ est linéaire, s'annule en 0, et reste positive sur [0;10].
$-3r+20$ est affine, de coefficient directeur $-3$, et s'annule en ${20}/{3}$.
D'où le tableau de variation de $f$.
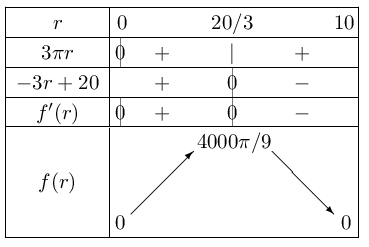
- Le tableau précédent donne les variations du volume du cylindre en fonction de son rayon.
Le volume du cylindre est maximum pour $r={20}/{3}≈6,67$ mètres.
Il est alors égal à ${4000π}/{9}≈1396$ $m^3$