Variations
Exercice 4
Dans ce problème, toutes les sommes d'argent sont exprimées en euros.
Une entreprise fabrique des véhicules pendant une semaine.
Soit $C(x)$ le coût total de production de $x$ véhicules.
La capacité de production ne dépasse pas $1\,500$ véhicules par semaine.
Dans tout ce qui suit, les fonctions seront définies sur des intervalles de $ℝ$,
mais évidemment, seules les valeurs entières des abscisses correspondent à des nombres de véhicules!
- La fonction $C$ est représentée ci-dessous par la courbe $\C$.
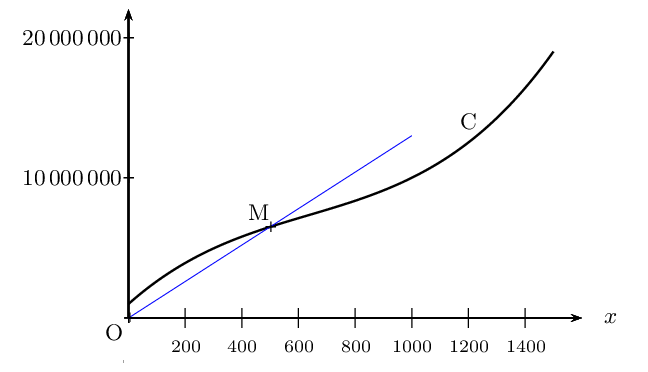
Le point O est l'origine du repère.
Le point M de la courbe $\C$ a pour coordonnées $(x;C(x))$.
Le coût moyen de production (pour $x$ véhicules fabriqués) est alors donné par la fonction:
$$f(x)={C(x)}/{x}$$
Quel lien y a-t-il entre la valeur de $f(x)$ et la droite (OM)?
L'optimum technique $x_{Opt-Tec}$ est la production assurant le coût moyen le plus faible.
Déterminer graphiquement une valeur approchée de l'optimum technique pour cette entreprise? -
On admet que: $C(x)=0,01x^3-19x^2+18\,000x+1\,000\,000$
Montrer que: $f\,'(x)={(x-1\,000)(0,02x^2+x+1\,000)}/{x^2}$.
- Montrer que, sur l'intervalle $]0;1\,500]$, $f\,'(x)$ est du signe de $x-1\,000$.
- Déterminer le tableau de variation de $f$ sur l'intervalle $]0;1\,500]$.
- Quelle est la valeur exacte de $x_{Opt-Tec}$? Quel est alors le coût moyen de production de chaque véhicule?
- Montrer alors que la tangente $d$ à la courbe $\C$ en $x_{Opt-Tec}$ passe par l'origine.
- Montrer que: $C\,'(x_{Opt-Tec})=f(x_{Opt-Tec})$.
Nous allons retrouver ci-après ce résultat par le calcul.
Solution...
Corrigé
-
On a: $f(x)={C(x)}/{x}={C(x)-0}/{x-0}={y_M-y_O}/{x_M-x_O}$
On reconnaît le coefficient directeur de la droite (OM).
Et ce coefficient sera minimal si M est confondu avec le point A du dessin ci-dessous; en effet, la droite (OM) a alors sa "pente" la plus faible.
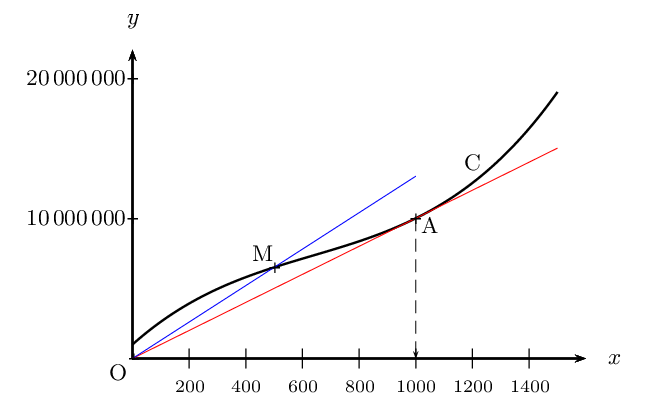
On obtient alors une valeur de $x_{Opt-Tec}$ qui semble être proche de $1\,000$.
L'optimum technique est sans doute proche de $1\,000$ véhicules produits par semaine. -
On a: $f(x)={C(x)}/{x}$.
Donc: $f\,'(x)={C'(x)×x-C(x)×1}/{x^2}$
On calcule alors: $C'(x)=0,01×3x^2-19×2x+18\,000=0,03x^2-38x+18\,000$.
On obtient donc: $f\,'(x)={(0,03x^2-38x+18\,000)×x-(0,01x^3-19x^2+18\,000x+1\,000\,000)}/{x^2}$
Soit: $f\,'(x)={0,03x^3-38x^2+18\,000x-0,01x^3+19x^2-18\,000x-1\,000\,000}/{x^2}$
Soit: $f\,'(x)={0,02x^3-19x^2-1\,000\,000}/{x^2}$
Or: ${(x-1\,000)(0,02x^2+x+1\,000)}/{x^2}={x×0,02x^2+x×x+x×1\,000-1\,000×0,02x^2-1\,000×x-1\,000×1\,000}/{x^2}$
Soit: ${(x-1\,000)(0,02x^2+x+1\,000)}/{x^2}={0,02x^3+x^2+1\,000x-20x^2-1\,000x-1\,000\,000}/{x^2}$
Soit: ${(x-1\,000)(0,02x^2+x+1\,000)}/{x^2}={0,02x^3-19x^2-1\,000\,000}/{x^2}$
Donc: $f\,'(x)={(x-1\,000)(0,02x^2+x+1\,000)}/{x^2}$.
A retenir: pour montrer une égalité du type $a=b$, il suffit de montrer qu'il existe $c$ tel que $a=c$ et $b=c$.
- $f\,'(x)$ se présente sous forme d'un quotient.
Son dénominateur $x^2$ est un carré; il est donc positif. Il est même strictement positif sur l'intervalle $]0;1\,500]$.
Donc le quotient $f\,'(x)$ est du signe de son numérateur $(x-1\,000)(0,02x^2+x+1\,000)$.
Ce numérateur est un produit de 2 facteurs.
Le second facteur $0,02x^2+x+1\,000$ est un trinôme avec $a=0,02$, $b=1$ et $c=1\,000$.
$Δ=b^2-4ac=1^2-4×0,02×1\,000=-79$.
$Δ$<$0$. Donc le trinôme reste du signe de $a$, c'est à dire strictement positif.
Donc le numérateur est du signe de son premier facteur $x-1\,000$.
Et par là, $f\,'(x)$ est du signe de $x-1\,000$. - On a vu que $f\,'(x)$ est du signe de $x-1\,000$.
Or $x-1\,000$ est une fonction affine.
Cette fonction s'annule pour $x=1\,000$, et son coefficient directeur est strictement positif (il vaut $1$).
D'où le tableau de variation de $f$ sur l'intervalle $]0;1\,500]$.
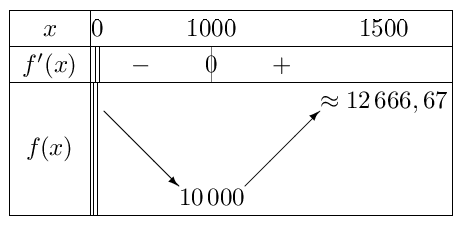
On notera que: $f(1\,000)={C(1\,000)}/{1\,000}=10\,000$ et que $f(1\,500)={C(1\,500)}/{1\,500}≈12\,666,67$ - D'après le tableau de variation ci-dessus, $f$ admet un minimum en $x_{Opt-Tec}=1\,000$.
L'optimum technique est est donc égal à $1\,000$ véhicules produits par semaine.
Le coût moyen de production de chaque véhicule est alors de $10\,000$ euros. - La tangente $d$ à la courbe $\C$ en $x_0$ a pour équation: $y=C(x_0)+C\,'(x_0)(x-x_0)$.
Or: $x_0=1\,000$, $C(x_0)=10\,000\,000$. Et $C\,'(x_0)=0,03×1\,000^2-38×1\,000+18\,000=10\,000$.
Donc $d$ a pour équation: $y=10\,000\,000+10\,000(x-1\,000)$.
Soit: $y=10\,000\,000+10\,000x-10\,000\,000$.
Soit: $y=10\,000x$.
L'ordonnée à l'origine est donc nulle.
Donc $d$ passe bien par l'origine. - On a vu que $C\,'(x_{Opt-Tec})=C\,'(1\,000)=10\,000$.
Or $f(x_{Opt-Tec})=f(1\,000)=10\,000$.
Donc on a bien: $C\,'(x_{Opt-Tec})=f(x_{Opt-Tec})$.
Cette égalité traduit le fait qu'en $x_{Opt-Tec}$, la tangente à $\C$ et la corde (OM) sont confondues.