 Variations
Variations
Exercice 5
Dans ce problème, toutes les sommes d'argent sont exprimées en euros.
Une entreprise fabrique des véhicules pendant une semaine.
Soir $C(x)$ le coût total de production de $x$ véhicules.
La capacité de production ne dépasse pas $1\,500$ véhicules par semaine.
Soit $R(x)$ les recettes générées par la vente de $x$ véhicules.
Soit $b(x)$ le gain obtenu si l'entreprise a fabriqué et vendu $x$ véhicules.
Si $b(x)$>$0$, alors $b(x)$ représente un bénéfice; si $b(x)$<$0$, alors $b(x)$ représente une perte.
Dans tout ce qui suit, les fonctions seront définies sur des intervalles de $ℝ$,
mais évidemment, seules les valeurs entières des abscisses correspondent à des nombres de véhicules!
- La fonction $C$ est représentée ci-dessous par la courbe $\C$.
La fonction $R$ est représentée ci-dessous par la courbe $\R$.
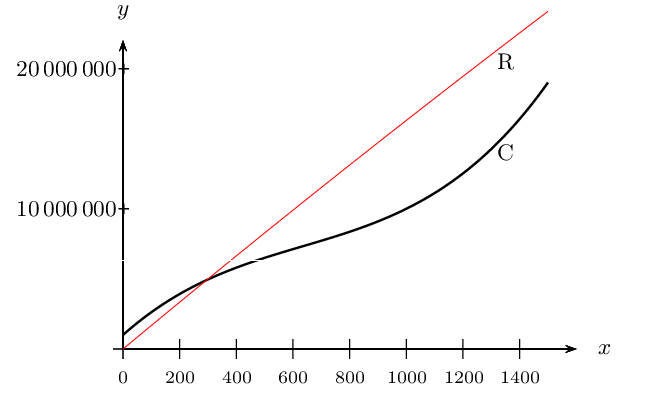
Déterminer graphiquement le nombre de véhicules à produire et à vendre pour que l'entreprise n'ait pas de pertes.
L'optimum économique $x_{Opt-Eco}$ est la production assurant le profit maximal.
Déterminer graphiquement une valeur approchée de l'optimum économique pour cette entreprise? -
On admet que: $C(x)=0,01x^3-19x^2+18\,000x+1\,000\,000$
On admet que: $R(x)=-0,5x^2+16\,800x$
Montrer que: $b\,'(x)=-0,03x^2+37x-1\,200$. - Déterminer le tableau de variation de $b$ sur l'intervalle $[0;1\,500]$.
- Déterminer la valeur exacte de l'optimum économique $x_{Opt-Eco}$? Quel est alors le bénéfice moyen sur chaque véhicule vendu?
- Par essais successifs, déterminer le nombre de véhicules à produire et à vendre pour que l'entreprise n'ait pas de pertes.
- Montrer que: $C\,'(x_{Opt-Eco})=R\,'(x_{Opt-Eco})$.
Nous allons retrouver ci-après ces résultats par le calcul.
Solution...
Corrigé
- Recherches graphiques.
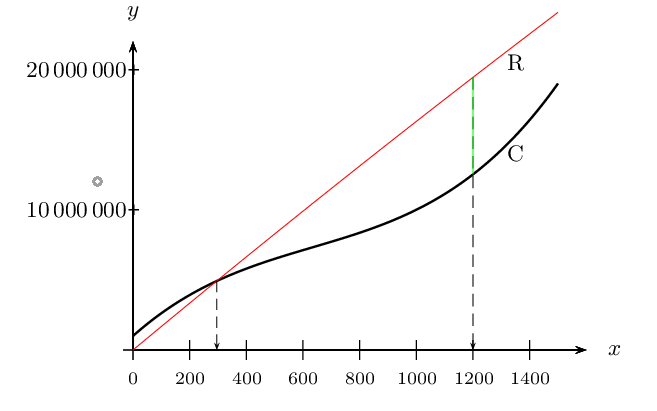
L'entreprise n'a pas de pertes lorsque $R(x)≥C(x)$.
Graphiquement, on peut donc estimer que l'entreprise doit produire au moins 300 véhicules environ pour éviter les pertes.
Le profit est maximal lorsque la différence $R(x)-C(x)$ est la plus grande.
Graphiquement, on peut donc estimer que l'optimum économique $x_{Opt-Eco}$ est proche de $1\,200$ véhicules.
-
On a: $b(x)=R(x)-C(x)=-0,5x^2+16\,800x-(0,01x^3-19x^2+18\,000x+1\,000\,000)$.
Soit: $b(x)=-0,5x^2+16\,800x-0,01x^3+19x^2-18\,000x-1\,000\,000$.
Soit: $b(x)=-0,01x^3+18,5x^2-1\,200x-1\,000\,000$.
Donc: $b\,'(x)=-0,01×3x^2+18,5×2x-1\,200$.
Soit: $b\,'(x)=-0,03x^2+37x-1\,200$. - $b\,'(x)$ se présente sous forme d'un trinôme avec $a=-0,03$, $b=37$ et $c=-1\,200$.
$Δ=b^2-4ac=37^2-4×(-0,03)×(-1\,200)=1\,225$.
$Δ$>$0$. Donc le trinôme a deux racines: $x_1={-b-√Δ}/{2a}={-37-√{1\,225}}/{-0,06}=1\,200$ et $x_2={-b+√Δ}/{2a}={-37+√{1\,225}}/{-0,06}≈33,33$.
La forme factorisée de $b\,'(x)$ est $-0,03(x-x_1)(x-x_2)$.
Et comme $a$<$0$, on obtient facilement le tableau de variation suivant.
Nous n'avons pas fait apparaitre les facteurs par soucis de lisibilité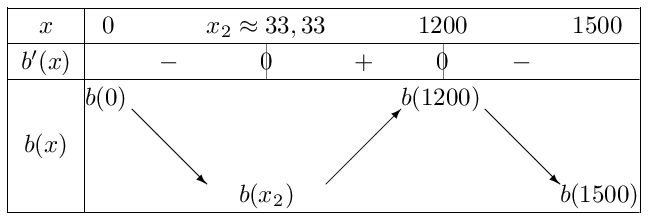
On notera que: $b(0)=-1\,000\,000$, $b(x_2)≈-1\,019\,814,82$, $b(1\,200)=6\,920\,200$ et que $b(1\,500)=5\,075\,000$ - D'après le tableau de variation ci-dessus, $b$ admet un maximum en $x_{Opt-Eco}=1\,200$.
L'optimum économique est est donc égal à $1\,200$ véhicules produits et vendus par semaine.
Le bénéfice moyen sur chaque véhicule vendu est alors égal à: ${b(1\,200)}/{1\,200}={6\,920\,200}/{1\,200}≈5\,766,83$ euros. - D'après le tableau de variation précédent, l'entreprise subit des pertes si elle produit et vend peu de véhicules.
Mais, dès que la production dépasse une certaine valeur, l'entreprise réalise des bénéfices.
Or on constate que: $b(295)≈-761$ et que $b(296)≈6\,353$.
Donc l'entreprise doit fabriquer et vendre au moins 296 véhicules pour commencer à avoir un bénéfice.
On notera qu'à la capacité maximale de l'usine, soit $1\,500$ véhicules par semaine, l'entreprise réalise toujours un bénéfice. - On a: $C'(x)=0,01×3x^2-19×2x+18\,000=0,03x^2-38x+18\,000$.
On obtient alors: $C\,'(x_{Opt-Eco})=C\,'(x_{1\,200})=15\,600$.
De même, on a: $R\,'(x)=-x+16\,800$.
On obtient alors: $R'(x_{Opt-Eco})=15\,600$
Donc on a bien: $C\,'(x_{Opt-Eco})=R\,'(x_{Opt-Eco})$.
Les économistes approximent souvent la recette marginale par $R\,'(x)$ et le coût marginal par $C'(x)$. Donc l'égalité obtenue traduit le fait qu'en $x_{Opt-Eco}$, recette marginale et coût marginal sont égaux.