Variations
Variations
Exercice 7
Un canon, placé au sol sur un terrain parfaitement horizontal, tire un boulet. La trajectoire du boulet reste dans un plan vertical.
Ce plan est rapporté à un repère orthonormé (O, I, J).
L'axe (OI) est horizontal, l'axe (OJ) est vertical.
Le canon est en O. L'angle de tir par rapport à l'horizontale est $a$ (en degrés).
Les unités des axes sont les mètres.
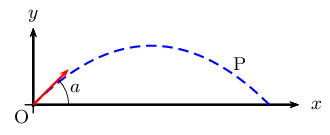
On appelle $P$ la trajectoire suivie par ce boulet.
On admettra que $P$ admet pour équation: $y=f(x)$ avec $f(x)=-{x^2}/{800}(1+(\tan (a))^2)+x\tan(a)$.
On rappelle que $\tan(a)={\sin(a)}/{\cos(a)}$
Partie A
Quelle est la nature de $f$? Quelle est la nature de $P$?
Partie B
On suppose dans cette partie que $a=45°$.
- Montrer que $f(x)=-0,0025x^2+x$
- Soit $\D_f$ le domaine de définition de $f$. Dans le cadre de ce problème, comme $f(x)$ représente une altitude, il est clair que $f(x)$ existe si et seulement si $f(x)≥0$.
Déterminer $\D_f$. - Déterminer $f'(x)$, puis dresser le tableau de variation de $f$ sur $\D_f$.
- Donner les coordonnées du sommet de $P$ et donner l'équation de son axe de symétrie.
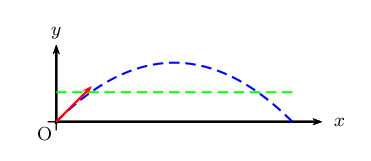
- Un drone vole horizontalement à 50 mètres d'altitude dans le plan de tir.
Déterminer les abscisses des points où le boulet peut l'atteindre.
Partie C
On revient au cas général.
- Un drone en vol stationnaire se situe dans le plan de tir au point $M(200;130)$.
Est-il possible que le boulet le touche si $a=45°$? - Pour atteindre le point $M(200;130)$ , l'artilleur devra choisir finement la hausse $a$ du canon, c'est-à-dire la valeur de $\tan(a)$
Posons $t=\tan(a)$.
Montrer que $t$ est solution de l'équation $50t^2-200t+180=0$ - Résoudre cette équation.
-
On admet que la touche Arctan de votre calculatrice permet, à partir de la valeur de $\tan a$, d'obtenir l'unique mesure de $a$ convenable entre -90° et 90° (il vaudrait mieux que cette mesure soit positive, sinon, l'artilleur va se tirer dans le pied!)
Déterminer les valeurs possibles de $a$ (arrondies au degré)
Solution...
Corrigé
Partie A
$f(x)=-{x^2}/{800}(1+(\tan (a))^2)+x\tan(a)$.
$f$ est un trinôme du second degré dont les coefficients sont: ${1+(\tan (a))^2}/{800}$, $\tan(a)$ et 0.
Et par là, comme le repère est orthonormé, sa représentation graphique $P$ est une parabole.
Partie B
- Ici $a=45°$. Donc $\tan(a)={\sin 45°}/{\cos 45°}={{√2}/{2}}/{{√2}/{2}}=1$.
Donc on obtient: $f(x)=-{x^2}/{800}(1+1^2)+x×1=-0,0025x^2+x$ - On cherche les valeurs de $x$ pour lesquelles on a $f(x)≥0$.
Or $f(x)=x(-0,0025x+1)$.
Ses racines sont alors $0$ et ${-1}/{-0,0025}=400$.
D'où le tableau de signes de $x(-0,0025x+1)$

Par conséquent $\D_f=[0;400]$. - On a: $f'(x)=-0,0025×2x+1=-0,005x+1$
$-0,005x+1$ est une fonction affine, de coefficient directeur $a$ strictement négatif, qui s'annule pour $x=200$.
D'où le tableau de variation de $f$ sur $ [0;400]$.
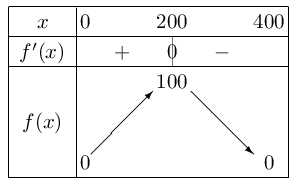
- Par conséquent, le sommet de $P$ a pour coordonnées (200;100).
Et $P$ admet pour axe de symétrie la droite d'équation $x=200$. - Un drone vole horizontalement à 50 mètres d'altitude dans le plan de tir.
Les abscisses des points où le boulet peut l'atteindre sont solutions de l'équation $f(x)=50$.
$f(x)=50$ $ ⇔$ $-0,0025x^2+x-50=0$
Le membre de gauche est un trinôme avec $a=-0,0025$, $b=1$ et $c=-50$.
$Δ=b^2-4ac=1^2-4×(-0,0025)×(-50)=0,5$.
$Δ>0$. Le trinôme a 2 racines $x_1={-b-√Δ}/{2a}={-1-√{0,5}}/{-0,005}≈341,4$ et $x_2={-b+√Δ}/{2a}{-1+√{0,5}}/{-0,005}≈58,6$.
Le boulet peut atteindre le drone en 2 points, dont les abscisses valent environ 58,86m et 341,4m
Partie C
On revient au cas général.
- Un drone en vol stationnaire se situe dans le plan de tir au point $M(200;130)$.
Il est donc situé à 130m de hauteur.
Or, si $a=45°$, alors l'altitude maximale du boulet est de 100m (d'après le tableau de variation de la partie B).
Donc le boulet ne peut pas atteindre le drone. -
Le boulet peut toucher le drone si et seulement si le point $M(200;130)$ fait partie de la parabole $P$.
C'est à dire lorsque $f(200)=130$
Soit: $-{200^2}/{800}(1+(\tan (a))^2)+200\tan(a)=130$
Posons $t=\tan(a)$.
On obtient alors: $-{200^2}/{800}(1+t^2)+200t=130$
Soit: $-50(1+t^2)+200t=130$
Soit: $-50-50t^2+200t=130$
Et finalement: $0=50t^2-200t+180$ C'est l'équation prévue. -
Le membre de gauche est un trinôme avec $a=50$, $b=-200$ et $c=180$.
$Δ=b^2-4ac=(-200)^2-4×50×180=4000$.
$Δ>0$. Le trinôme a 2 racines $t_1={-b-√Δ}/{2a}={200-√{4000}}/{100}≈1,368$ et $t_2={200+√{4000}}/{100}≈2,632$. -
A l'aide de la calculatrice, on obtient $a≈54°$ ou $a≈69°$
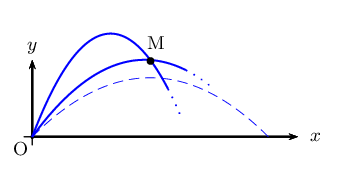
On a tracé ci-dessous les 2 paraboles corespondant aux 2 angles de tir possibles.
Pour mémoire, la parabole P de la partie B est également représentée (en traits interrompus)