 Les fonctions affines
Les fonctions affines
I. Fonctions affines $f(x)=ax+b$
Propriété 1
La fonction affine est définie sur $\ℝ$.
Une fonction $f$ est affine si et seulement si elle est représentée par une droite.
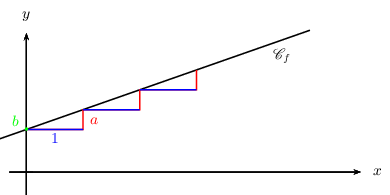
La fonction affine $f(x)=ax+b$ est représentée par la droite d'équation $y=ax+b$.
Cette droite a pour ordonnée à l'origine le nombre $b$. Cela signifie qu'elle passe par le point de coordonnées $(0;b)$.
Cette droite a coefficient directeur le nombre $a$.
Le coefficient directeur représente la pente de la droite
(il est positif si la droite "monte", négatif si la droite "descend", et nul si la droite est "horizontale").
Exemple 1
Représenter la fonction $f(x)=2x+1,5$
Corrigé
$f$ est affine. Elle est représentée par la droite passant par $(\,0\,;\,1,5\,)$ dont le coefficient directeur vaut 2.
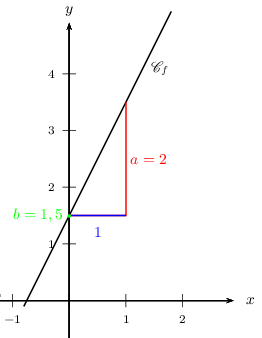
Pour tracer la droite, on a placé le point $(\,0\,;\,1,5\,)$.
Puis, pour trouver un second point, on a avancé de 1 "horizontalement vers la droite", et on a monté de 2.
Exemple 2
Représenter la fonction $g(x)=-0,1x+2$
Corrigé
$g$ est affine. Elle est représentée par la droite d'ordonnée à l'origine 2, et dont le coefficient directeur vaut $-0,1$.
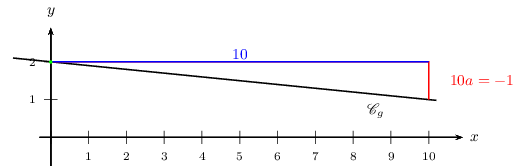
Pour tracer la droite, on a placé le point $(\,0\,;\,2\,)$.
Puis, pour trouver un second point, on aurait pu avancer de 1 "horizontalement vers la droite", puis descendre de $0,1$. Cela aurait été imprécis.
On a préféré avancer de 10 "horizontalement vers la droite", puis descendre de 10 fois $0,1$, c'est à dire de $1$.
Propriété 2
Dans le plan rapporté à un repère, la droite (AB) admet pour coefficient directeur ${y_B-y_A}/{x_B-x_A}$
Exemple
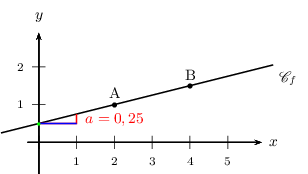
Déterminer la fonction $f$ représentée par la droite (AB) où $A(\,2\,;\,1\,)$ et $B(\,4\,;\,1,5\,)$
Corrigé
La fonction $f$ est représentée par une droite, donc elle est affine, et donc $f(x)=ax+b$ (où $a$ et $b$ sont fixés).
Comme la droite passe par A et B, on a: $a={y_B-y_A}/{x_B-x_A}$
Soit: $a={1,5-1}/{4-2}=0,25$
Et donc: $f(x)=0,25x+b$
Comme la droite passe par A, on a: $f(x_A)=y_A$
Soit: $0,25×2+b=1$, et par là: $0,5+b=1$, et donc: $b=1-0,5=0,5$
Par conséquent: $f(x)=0,25x+0,5$
Voici un graphique convenable (non demandé)
Propriété 3
On considère la fonction affine $f$ définie par $f(x)=ax+b$ pour tout réel $x$.
$f$ est strictement croissante si et seulement si $a>0$
$f$ est strictement décroissante si et seulement si $a<0$
$f$ est constante si et seulement si $a=0$
Opérations, égalités et inégalités
Si $a=b$ et $c=d$, alors $a+c=b+d$
Pour tout réel $k$ non nul, on a: $a=b$ $⇔$ $ka=kb$
Si $a≤b$ et $c≤d$, alors $a+c≤b+d$
Pour tout réel $k$ strictement positif, on a: $a≤b$ $⇔$ $ka+c≤kb+c$
Cela tient à la stricte croissance de la fonction $kx+c$ pour $k>0$
Pour tout réel $k$ strictement négatif, on a: $a≤b$ $⇔$ $ka+c≥kb+c$
Cela tient à la stricte décroissance de la fonction $kx+c$ pour $k<0$
On obtient des propriétés analogues en remplaçant $≤$ par $<$, $≥$ ou $>$.
Exemple
On suppose que $-2≤x≤3$. Encadrons $-4x+1$
On a: $-2≤x≤3$.
Et comme $-4<0$, on obtient: $(-4)×(-2)+1≥-4x+1≥(-4)×3+1$
Soit: $9≥-4x+1≥-11$
Propriété 4
Etude du signe de $f(x)=ax+b$
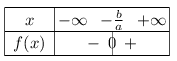
Si $a>0$, alors la fonction affine $f(x)=ax+b$ est strictement croissante.
Or $ax+b=0$ $⇔$ $x=-{b}/{a}$
Donc on obtient le tableau de signes suivant:
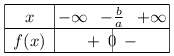
Si $a<0$, alors la fonction affine $f(x)=ax+b$ est strictement décroissante.
Or $ax+b=0$ $⇔$ $x=-{b}/{a}$
Donc on obtient le tableau de signes suivant:
Exemple
- Déterminer le signe de $f(x)=2x+7$ en fonction de $x$
- Sans calcul, déterminer le signe de $f(-π)$
Corrigé
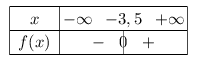
- Comme $2>0$, la fonction affine $f(x)=2x+7$ est strictement croissante.
Or $2x+7=0$ $⇔$ $x=-{7}/{2}=-3,5$
Donc on obtient le tableau de signes suivant:
- On a: $π<3,5$, et donc $-π>-3,5$
Donc, d'après le tableau de signes ci-dessus, on a: $f(-π)>0$
Les coefficients directeurs de droites seront particulièrment utiles en géométrie.
L'étude du signe de fonctions affines sera souvent déterminante pour trouver le signe d'une expression plus complexe, à condition de savoir factoriser...
II. Fonctions affines particulières
Définition
On considère la fonction affine $f$ définie par $f(x)=ax+b$ pour tout réel $x$.
Si $b=0$, alors $f(x)=ax$, et la fonction $f$ est linéaire.
Une fonction linéaire traduit une situation de proportionnalité.
Si $a=0$, alors $f(x)=b$, et la fonction $f$ est constante.
III. Equations et inéquations
a. Equations
Définition
Une équation du type $ax+b=0$, où $a$ et $b$ sont deux réels fixés (avec $a≠0$), s'appelle une équation du premier degré .
Méthode de résolution d'une équation
Après une éventuelle transposition, toute équation peut s'écrire sous la forme $f(x)=0$.
Avant de résoudre une telle équation, il faut déterminer le domaine de définition de $f$ (pour repérer les valeurs qui ne peuvent pas être des solutions (les valeurs "interdites")).
Le domaine de définition de $f$ s'appelle alors le domaine d'étude de l'équation et on le note généralement $\D_E$.
Très souvent, il est évident que le domaine d'étude est $\ℝ$, et il courant de ne pas le citer.
Si (à une constante près) $f$ est une fonction de référence (par exemple une fonction affine), alors la résolution est évidente (voir exemple 1).
Sinon, il est conseillé de factoriser $f(x)$ ou de réduire au même dénominateur pour obtenir un produit ou un quotient.
Le but est de se ramener à la résolution d'une ou plusieurs équations de référence (par exemple des équations du premier degré) (voir exemples 2, 3 et 4)
Exemple 1
Résoudre l'équation (E): ${2}/{3}x-{1}/{4}={1}/{5}x+2$, puis interpréter graphiquement.
Corrigé
On annule le membre de droite.
(E) $⇔$ ${2}/{3}x-{1}/{5}x-{1}/{4}-2=0$
(E) $⇔$ $({2}/{3}-{1}/{5})x-{1}/{4}-{8}/{4}=0$
(E) $⇔$ $({10}/{15}-{3}/{15})x-{9}/{4}=0$
(E) $⇔$ ${7}/{15}x-{9}/{4}=0$
On constate que (E) est une équation du premier degré.
Il est facile d'isoler le $x$.
(E) $⇔$ ${7}/{15}x={9}/{4}$ (On a additionné ${9}/{4}$ à chaque membre)
(E) $⇔$ $x={9}/{4}×{15}/{7}$ (On a multiplié chaque membre par ${15}/{7}$)
(E) $⇔$ $x={9×15}/{4×7}={135}/{28}$
Donc $\S=\{\,{135}/{28}\,\}$
Interprétation graphique
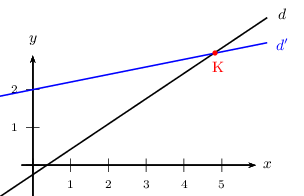
On trace la droite $d$ d'équation $y={2}/{3}x-{1}/{4}$. Elle passe par $(0;-{1}/{4})$ et a pour coefficient directeur ${2}/{3}$.
On trace la droite $d'$ d'équation $y={1}/{5}x+2$. Elle passe par $(0;2)$ et a pour coefficient directeur ${1}/{5}$.
Les droites $d$ et $d'$ se coupent au point K, dont l'abscisse ${135}/{28}≈4,8$ est solution de l'équation (E)
Exemple 2
a. Résoudre l'équation (E): $3x^2=x$
b. Voici les représentations graphiques des fonctions $f(x)=3x^2$ et $g(x)=x$
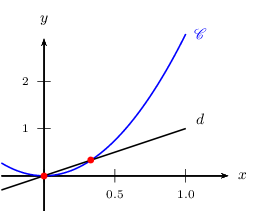
Interpréter graphiquement la résolution de (E)
Corrigé
a. Résolution
(E) $⇔$ $3x^2-x=0$ ((E) n'est pas une équation du premier degré; on factorise).
(E) $⇔$ $x(3x-1)=0$ (le membre de gauche est un produit, et il est égal à 0).
Un produit est nul lorsque l'un de ses facteurs est nul.
(E) $⇔$ $x=0$ ou $3x-1=0$ (on s'est ramené à deux équations du premier degré).
(E) $⇔$ $x=0$ ou $x={1}/{3}$
Donc $\S=\{\,0\,;\,{1}/{3}\,\}$
b. Interprétation graphique
(E) $⇔$ $f(x)=g(x)$
$g$, fonction linéaire, est représentée par une droite. Il s'git de la droite $d$ et, par élimination, $f$ est représentée par la courbe $C$ (il s'agit en fait d'une parabole).
La droite et la courbe se coupent en deux points (en rouge sur le graphique), dont les abscisses sont les solutions de l'équation (E).
Exemple 3
Résoudre l'équation (E): $x^2+2x=-1$
Corrigé
(E) $⇔$ $x^2+2x+1=0$ ((E) n'est pas une équation du premier degré; on factorise).
(E) $⇔$ $(x+1)^2=0$ (le membre de gauche est un produit, et il est égal à 0).
Un produit est nul lorsque l'un de ses facteurs est nul.
(E) $⇔$ $x+1=0$ ou $x+1=0$ (on s'est ramené à deux équations du premier degré semblables).
(E) $⇔$ $x=-1$
Donc $\S=\{\,-1\,\}$
Exemple 4
Résoudre l'équation (E): ${2}/{x+1}={1}/{x}-{1}/{x+1}$
Corrigé
Un quotient n'existe que lorsque son dénominateur est non nul. Donc ici, il y a des valeurs interdites; et il faut déterminer le domaine d'étude.
On doit avoir: $x+1≠0$ et $x≠0$
Soit: $x≠-1$ et $x≠0$. Donc $\D_E=ℝ\\\{-1;0\}$
(E) $⇔$ ${2}/{x+1}-{1}/{x}+{1}/{x+1}=0$ ((E) n'est pas une équation du premier degré; on réduit au même dénominateur).
(E) $⇔$ ${2x}/{x(x+1)}-{x+1}/{x(x+1)}+{x}/{x(x+1)}=0$
(E) $⇔$ ${2x-x-1+x}/{x(x+1)}=0$
(E) $⇔$ ${2x-1}/{x(x+1)}=0$
(le membre de gauche est un quotient, et il est égal à 0).
Un quotient est nul lorsque son numérateur est nul.
(E) $⇔$ $2x-1=0$ (on s'est ramené à une équation du premier degré)
(E) $⇔$ $x=0,5$ (cette valeur n'est pas interdite)
Donc $\S=\{\,0,5\,\}$
b. Inéquations
Méthode de résolution d'une inéquation
La méthode est similaire à celle permettant de résoudre des équations.
Il suffit de transposer certains termes et de se ramener à la résolution d'une inéquation de référence (voir exemple 1).
Si la méthode ne fonctionne pas, il est conseillé de transposer le membre de droite pour obtenir une inéquation du type $f(x)≤0$ (ou $f(x)<0$ ou $f(x)≥0$ ou $f(x)>0$).
Factoriser $f(x)$, ou l'écrire sous forme d'un quotient permet souvent de conclure; en effet, le signe d'un produit ou d'un quotient est souvent facile à déterminer (voir exemples 2 et 3).
Exemple 1
Résoudre l'inéquation (E): $x+7<4x+3$, puis interpréter graphiquement.
Corrigé
On reconnaît une inéquation du premier degré.
(E) $⇔$ $x-4x<3-7$
(E) $⇔$ $-3x<-4$
(E) $⇔$ $x>{-4}/{-3}$ (On a multiplié chaque membre par ${1}/{-3}$ (ou divisé chaque membre par $-3$) qui est strictement négatif, d'où le changement de sens de l'inéquation)
(E) $⇔$ $x>{4}/{3}$
Donc $\S=]\,{4}/{3}\,;\,+\∞\,[$
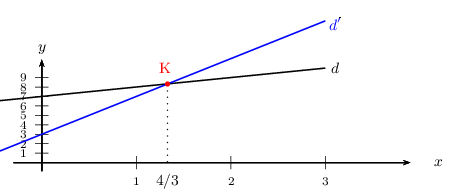
Interprétation graphique
On trace la droite $d$ d'équation $y=x+7$. Elle passe par $(0;7)$ et a pour coefficient directeur $1$.
On trace la droite $d'$ d'équation $y=4x+3$. Elle passe par $(0;3)$ et a pour coefficient directeur $4$.
$d$ et $d'$ se coupent au point K d'abscisse ${4}/{3}$
$d$ est en dessous de $d'$ pour les points dont les l'abscisses sont strictement supérieures à ${4}/{3}$
Exemple 2
a. Résoudre l'inéquation (E): $x<x^2$.
b. Voici les représentations graphiques des fonctions $f(x)=x$ et $g(x)=x^2$
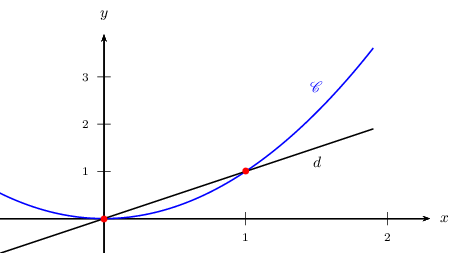
Interpréter graphiquement la résolution de (E)
Corrigé
a. Résolution
(E) $⇔$ $x-x^2<0$ ((E) n'est pas une inéquation du premier degré; on factorise).
(E) $⇔$ $x(1-x)<0$
(E) $⇔$ $x(-x+1)<0$
C'est alors que la méthode pour résoudre une inéquation devient différente de celle concernant les équations!
Nous allons déterminer le signe du produit $x(-x+1)$.
$x$ est une fonction linéaire, qui s'annule en 0, de coefficient directeur $1>0$.
$-x+1$ est une fonction affine, qui s'annule en 1, de coefficient directeur $-1<0$.
D'où le tableau de signes:
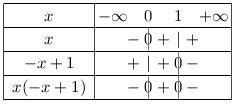
Or, on cherche les valeurs de $x$ pour lesquelles le produit est strictement négatif.
Donc $\S=]\,-\∞\,;0[\,∪\,]\,1\,;\,+\∞\,[$
b. Interprétation graphique
(E) $⇔$ $f(x)<g(x)$
$f$, fonction linéaire, est représentée par la droite. Par élimination, $g$ est représentée par la courbe $C$ (il s'agit en fait d'une parabole).
La droite est en dessous de la courbe pour les points dont les l'abscisses sont soit strictement inférieures à $0$, soit strictement supérieures à $1$.
Exemple 3
Résoudre l'inéquation (E): ${11x+7}/{-3x+5}≥0$.
Corrigé
Un quotient n'existe que lorsque son dénominateur est non nul. Donc ici, il y a des valeurs interdites; et il faut déterminer le domaine d'étude.
On doit avoir: $-3x+5≠0$
Soit: $x≠{-5}/{-3}$
Soit: $x≠{5}/{3}$
Donc $\D_E=ℝ\\\{{5}/{3}\}$
(E) $⇔$ ${11x+7}/{-3x+5}≥0$.
(E) n'est pas une inéquation du premier degré. Le membre de droite est déjà nul, et celui de gauche est déjà sous forme de quotient.
C'est alors que la méthode pour résoudre une inéquation devient différente de celle concernant les équations!
Nous allons déterminer le signe du quotient ${11x+7}/{-3x+5}$.
$11x+7$ est une fonction affine, qui s'annule en $-{7}/{11}$, de coefficient directeur $11>0$.
$-3x+5$ est une fonction affine, qui s'annule en ${5}/{3}$, de coefficient directeur $-3<0$.
D'où le tableau de signes:
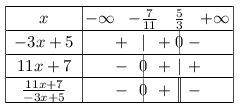
On note la double-barre, qui matérialise le fait que le quotient n'existe en ${5}/{3}$.
Or, on cherche les valeurs de $x$ pour lesquelles le quotient est positif (ou nul).
Donc $\S=[\,-{7}/{11}\,;\,{5}/{3}\,[$
On note que $-{7}/{11}$ fait partie des solutions, mais ${5}/{3}$ n'en fait pas partie.