Géométrie analytique non vectorielle
I Repérage dans le plan
Définition
Un repère du plan est défini par trois points non alignés $(O,I,J)$.
Si le triangle OIJ est rectangle en $O$, alors le repère est orthogonal.
Si, de plus, le triangle OIJ est isocèle en $O$, alors le repère est orthonormé (ou orthonormal).
Le repère est orthogonal lorsque les directions des axes sont perpendiculaires. Il est orthonormé lorsque les axes forment un angle droit et les unités sont les mêmes.
Propriété
Dans le plan rapporté à un repère $(O,I,J)$, tout point M est repéré par un un unique couple $(x_M;y_M)$ de nombres réels, appelé couple des coordonnées de M.
Remarque: on note indifféremment $M(x_M,y_M)$ ou $M(\table x_M; y_M)$.
Définition
La première coordonnée, $x_M$, est l'abscisse; la seconde coordonnée, $y_M$, est l'ordonnée.
II Coordonnées du milieu d'un segment
Le plan est muni d'un repère.
Propriété
Soit $A(x_A,y_A)$, $B(x_B,y_B)$ et $I(x_I,y_I)$ trois points du plan.
Le point I est le milieu du segment [AB]
si et seulement si
$x_I={x_A+x_B}/{2}$ et $y_I={y_A+y_B}/{2}$.
Exemple
Soit $A(\,1,6\,;\,0,8\,)$, $B(\,4,2\,;\,2,6\,)$, $C(\,3,2\,;\,-0,8\,)$ et $K(\,3,7\,;\,0,91\,)$.
Faire une figure.
Déterminer les coordonnées du milieu I du segment [AB].
Vérifier si K est le milieu du segment [BC].
Corrigé
Voici la figure demandée.
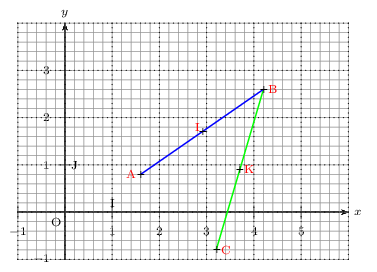
Ici, le repère est orthonormé (pour des raions de facilité), mais ce n'était pas exigé.
I est le milieu du segment [AB]
Donc: $x_I={x_A+x_B}/{2}$ et $y_I={y_A+y_B}/{2}$
Soit: $x_I={1,6+4,2}/{2}=2,9$ et $y_I={0,8+2,6}/{2}=1,7$
Donc: $I(\,2,9\,;\,1,7\,)$
Le milieu J du segment [BC] a pour coordonnées:
Donc: $x_J={x_B+x_C}/{2}$ et $y_J={y_B+y_C}/{2}$
Soit: $x_J={4,2+3,2}/{2}=3,7$ et $y_J={2,6+(-0,8)}/{2}=0,9$
Donc: $J(\,3,7\,;\,0,9\,)$
Et comme $y_K≠y_J$, K n'est pas le milieu de [BC].
III Distance entre deux points
Le plan est muni d'un repère orthonormé.
Propriété
Soit $A(x_A,y_A)$ et $B(x_B,y_B)$ deux points du plan.
La distance entre les points A et B est: $AB=√{(x_B-x_A)^2+(y_B-y_A)^2}$
Exemple
On reprend l'exemple précédent, et on suppose que le repère est orthonormé.
On rappelle que $A(\,1,6\,;\,0,8\,)$ et $B(\,4,2\,;\,2,6\,)$
Calculer la distance AB
Corrigé
On calcule: $(x_B-x_A)^2+(y_B-y_A)^2=(4,2-1,6)^2+(2,6-0,8)^2=2,6^2+1,8^2=10$
Donc, comme le repère est orthonormé, on obtient: $AB=√{10}≈3,16$