 La fonction carré $f(x)=x^2$
La fonction carré $f(x)=x^2$
Propriété 1
La fonction carré est définie sur $\ℝ$.
Dans un repère orthogonal, elle est représentée par une parabole, dont le "sommet" est l'origine du repère.
Cette parabole a pour axe de symétrie l'axe des ordonnées.
En effet, pour tout nombre $x$, on a: $f(-x)=f(x)$.
On dit que la fonction est paire.
Tableau de valeurs et représentation graphique

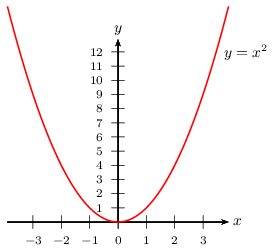
Propriété 2
La fonction carré admet le tableau de variation suivant.
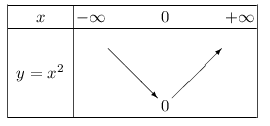
Exemple 1
On suppose que $2< x< 3$ et $-5< t< -4$.
Encadrer $x^2$ et $t^2$.
Corrigé
On a: $2< x< 3$
Donc: $2^2< x^2< 3^2$ ( car la fonction carré est strictement croissante sur [ $0$ ; $+\∞$ [ )
Soit: $4< x^2< 9$
On a: $-5< t< -4$
Donc: $(-5)^2> t^2>(-4)^2$ ( car la fonction carré est strictement décroissante sur ] $-\∞$ ; $0$ ] )
Soit: $25> t^2> 16$
Propriété 3
La fonction carré admet le tableau de signes suivant.
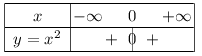
On notera qu'un carré est toujours positif (ou nul).
Equations et inéquations
Les équations et inéquations de référence concernant la fonction carré sont du type:
$x^2=k$ , $x^2<k$ , $x^2≤k$ ,
$x^2>k$ et $x^2≥k$ (où $k$ est un réel fixé).
Elles se résolvent facilement si l'on connaît l'allure de la parabole représentant la fonction carré (voir l'exemple 2).
La maîtrise de ces équations et inéquations permet de résoudre les équations ou inéquation du type:
$(f(x))^2=k$ et $(f(x))^2<k$ et celles obtenues en remplaçant $<$ par $≤$ ou $>$ ou $≥$ (où $k$ est un réel fixé et $f$ une fonction "simple") (voir l'exemple 3).
Exemple 2
- Résoudre l'équation $x^2=10$
- Résoudre l'inéquation $x^2≤10$
- Résoudre l'inéquation $x^2≥10$
Corrigé
-
$x^2=10$ $⇔$ $x=√{10}$ ou $x=-√{10}$
S$=\{-√{10};√{10}\}$
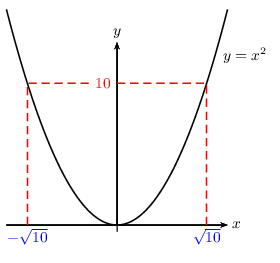
A retenir: si $a≥0$, alors: $x^2=a$ $⇔$ $x=√a$ ou $x=-√a$. -
$x^2≤10$ $⇔$ $-√{10}≤x≤√{10}$
S$=\[-√{10};√{10}\]$
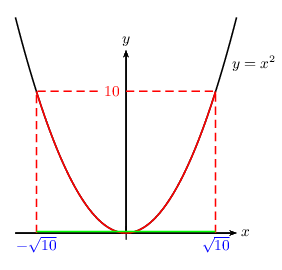
A retenir: si $a≥0$, alors: $x^2≤a$ $⇔$ $-√a≤x≤√a$. -
$x^2≥10$ $⇔$ $x≤-√{10}$ ou $x≥√{10}$
S$=]-\∞;-√{10}$$]∪[$$√{10};+\∞[$
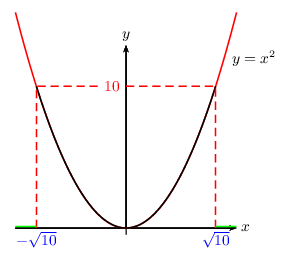
A retenir: si $a≥0$, alors: $x^2≥a$ $⇔$ $x≤-√{a}$ ou $x≥√{a}$.
Exemple 3
Résoudre l'équation $(2x+1)^2=9$
Corrigé
$(2x+1)^2=9$ $⇔$ $2x+1=√{9}$ ou $2x+1=-√{9}$
$⇔$ $2x=3-1$ ou $2x=-3-1$
$⇔$ $x={2}/{2}=1$ ou $x={-4}/{2}=-2$
S$=\{-2;1\}$
La méthode de résolution vue dans le cours sur les fonctions affines fonctionne également, mais elle est beaucoup plus longue.
On obtiendrait : $(2x+1)^2=9$ $⇔$ $(2x+1)^2-9=0$ $⇔$ $(2x+1)^2-3^=0$
$⇔$ $(2x+1-3)(2x+1+3)=0$ $⇔$ $(2x-2)(2x+4)=0$
$⇔$ $2x-2=0$ ou $2x+4=0$ $⇔$ $x=1$ ou $x=-2$
On retrouverait évidemment les solutions trouvées avec la première méthode !
A retenir
Quand un carré apparaît dans une équation ou une inéquation, il faut l'isoler si possible pour résoudre en utilisant la fonction carré.
Sinon, il faut revenir à la méthode vue dans le cours sur les fonctions affines (qui nécessite souvent une factorisation).