 Droites du plan - Systèmes linéaires
Droites du plan - Systèmes linéaires
I. Equations de droites
Propriété 1
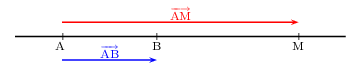
Soient A et B deux points distincts du plan.
La droite (AB) est l'ensemble des points M du plan tels que les vecteurs ${AB}↖{→}$ et ${AM}↖{→}$ soient colinéaires.
Définition
Soit ${u}↖{→}$ un vecteur non nul et $d$ une droite.
${u}↖{→}$ est un vecteur directeur de $d$
si et seulement si
il existe deux points distincts A et B de $d$ tels que ${AB}↖{→}$ et ${u}↖{→}$ sont colinéaires.

Propriété 2
Soient A un point et ${u}↖{→}$ un vecteur non nul.
La droite passant par A et de vecteur directeur ${u}↖{→}$ est l'ensemble des points M du plan tels que les vecteurs ${u}↖{→}$ et ${AM}↖{→}$ soient colinéaires.

On remarque qu'une droite admet une infinité de vecteurs directeurs, tous non nuls et colinéaires.
Propriété 3
Soient $d$ et $d'$ deux droites de vecteurs directeurs respectifs ${u}↖{→}$ et ${u'}↖{→}$.
$d$ est parallèle à $d'$ $⇔$ ${u}↖{→}$ et ${u'}↖{→}$ sont colinéaires.
Dans tout ce qui suit, le plan est muni d'un repère.
Propriété 4
Si une droite $d$ a pour vecteur directeur ${u}↖{→}(-b;a)$, alors elle admet une équation du type $ax+by+c=0$ , où $c$ est un réel fixé.
"Réciproquement".
Si $a$, $b$ et $c$ sont des réels fixés tels que $(a;b)≠(0;0)$,
alors l'ensemble des points dont les coordonnées vérifient l'équation $ax+by+c=0$
est une droite $d$ de vecteur directeur
${u}↖{→}(-b;a)$
L'équation $ax+by+c=0$ est dite équation cartésienne de la droite $d$.
Exemple
- Tracer la droite $d$ d'équation cartésienne $2x-3y+1=0$
- Donner un vecteur directeur ${u}↖{→}$ de la droite $d$.
- Le point $N(4;3)$ est-il sur $d$?
- Le point $P(5;7)$ est-il sur $d$?
Corrigé
-
Pour trouver 2 points de $d$, il suffit, par exemple,
de remplacer $x$ par 0 dans l'équation cartésienne, et de déterminer $y$,
ou de remplacer $y$ par 0, et de déterminer $x$
Ainsi, $x=0$ donne: $2×0-3y+1=0$, et par là: $y={1}/{3}$
et $y=0$ donne: $2x-3×0+1=0$, et par là: $x={-1}/{2}$
La droite $d$ passe par les points $A(0;{1}/{3})$ et $B({-1}/{2};0)$.
D'où le tracé qui suit.
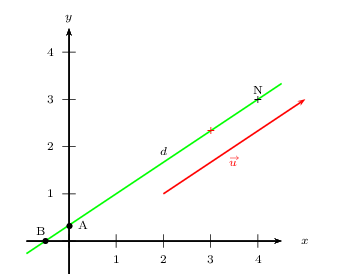
Comme les 2 points proposés sont proches, on peut en chercher un troisième, en posant, par exemple, $x=3$, ce qui donne $y={7}/{3}$ (la croix rouge sur le graphique)
- $d$ a pour équation cartésienne $2x-3y+1=0$.
On pose: $a=2$, $b=-3$ et $c=1$.
$d$ a pour vecteur directeur ${u}↖{→}(-b;a)$
Soit: ${u}↖{→}(3;2)$
- On calcule: $2x_N-3y_N+1=2×4-3×3+1=0$
Les coordonnées de N vérifient bien l'équation cartésienne de $d$.
Donc le point $N(4;3)$ est sur $d$. - On calcule: $2x_P-3y_P+1=2×5-3×7+1=-10$
Donc: $2x_P-3y_P+1≠0$
Les coordonnées de P ne vérifient pas l'équation cartésienne de $d$.
Donc le point $P(5;7)$ n'est pas sur $d$.
Propriété 5
Soit $d$ la droite du plan d'équation cartésienne $ax+by+c=0$
Si $b≠0$, alors $d$ a pour équation réduite: $y={-a}/{b}x-{c}/{b}$
Son coefficient directeur est égal à ${-a}/{b}$
Si $b=0$, alors $d$ a pour équation réduite: $x=-{c}/{a}$
$d$ est alors parallèle à l'axe des ordonnées, et elle n'a pas de coefficient directeur.
Exemple
Déterminer une équation cartésienne de la droite $d$ passant par $A(-1;1)$ et de vecteur directeur ${u}↖{→}(3;2)$.
En déduire son équation réduite.
Corrigé
Méthode 1
Comme $d$ a pour vecteur directeur ${u}↖{→}(3;2)$, on pose: $-b=3$ et $a=2$.
Ce qui donne: $a=2$ et $b=-3$
Donc $d$ a une équation du type: $2x-3y+c=0$.
Et, comme $d$ passe par $A(-1;1)$, on obtient: $2×(-1)-3×1+c=0$.
Et par là: $c=5$
Donc $d$ a pour équation cartésienne: $2x-3y+5=0$.
Méthode 2
$M(x;y)∈d$ $⇔$ ${AM}↖{→}$ et ${u}↖{→}$ sont colinéaires.
Or ${AM}↖{→}$ a pour coordonnées: $(x+1;y-1)$.
Et ${u}↖{→}$ a pour coordonnées: $(3;2)$.
Donc: $M(x;y)∈d$ $⇔$ $(x+1)×2-3×(y-1)=0$
Donc: $M(x;y)∈d$ $⇔$ $2x+2-3y+3=0$
Donc: $M(x;y)∈d$ $⇔$ $2x-3y+5=0$
Ceci est une équation cartésienne de la droite $d$.
On note que: $2x-3y+5=0$ $⇔$ $-3y=-2x-5$ $⇔$ $y={-2x-5}/{-3}$ $⇔$ $y={2}/{3}x+{5}/{3}$
Quelque soit la méthode choisie pour trouver une équation cartésienne, on en déduit l'équation réduite:
$y={2}/{3}x+{5}/{3}$
Attention !
Une droite admet une unique équation réduite mais une infinité d'équations cartésiennes (toutes proportionnelles).
On note que, si ${u}↖{→}(-b;a)$ et ${u'}↖{→}(-b';a')$, alors $det({u}↖{→},{u'}↖{→})=a'b-ab'$
D'où la propriété qui suit.
Propriété 6
Deux droites d'équations cartésiennes $ax+by+c=0$ et $a'x+b'y+c'=0$ sont parallèles
si et seulement si
$ab'-a'b=0$
Exemple
Les droites d'équation cartésienne ${2}/{3}x-{5}/{7}y+{11}/{13}=0$ et $-{8}/{7}x+{9}/{8}y+{11}/{13}=0$ sont-elles parallèles?
Corrigé
On pose: $a={2}/{3}$, $b=-{5}/{7}$ et $a'=-{8}/{7}$, $b'={9}/{8}$.
On calcule $ab'-a'b={2}/{3}×{9}/{8}-(-{8}/{7})×(-{5}/{7})={18}/{24}-{40}/{49}=-{13}/{196}$
Donc: $ab'-a'b≠0$
Donc les droites ne sont pas parallèles.
II. Résolution de systèmes linéaires
Définition
Un système linéaire de deux équations à deux inconnues $x$ et $y$ peut s'écrire sous la forme
$\{\table ax,+,by,+,c,=,0;a'x,+,b'y,+,c',=,0$
où $a$, $b$ et $c$ sont des réels fixés tels que $(a;b)≠(0;0)$,
et où $a'$, $b'$ et $c'$ sont des réels fixés tels que $(a';b')≠(0;0)$,
Propriété
On considère le système (S): $\{\table ax,+,by,+,c,=,0;a'x,+,b'y,+,c',=,0$
(S) admet un unique couple solution
si et seulement si les droites d'équations $ax+by+c=0$ et $a'x+b'y+c'=0$ sont sécantes
si et seulement si $ab'-a'b≠0$
Dans ce cas, les droites considérées se coupent au point dont le couple de coordonnées est solution du système.
Propriété
Un système linéaire de deux équations à deux inconnues peut se résoudre par substitution ou par combinaisons linéaires (voir exemple suivant). Le principe est toujours d'éliminer une inconnue dans certaines équations.
Exemple
Le plan est rapporté à un repère orthonormé (O,I,J).
1.Tracer les droites associées au système: (S): $\{\table x-3y+3=0; x-y-1=0$
2. Résoudre graphiquement le système précédent.
3. Après avoir vérifié par un calcul rapide que le système a bien une solution unique, résoudre algébriquement ce système.
Corrigé
1.
Méthode 1: A savoir: une égalité du type $ax+by+c=0$
(avec $a$ et $b$ non tous les deux nuls) est une équation cartésienne de droite.
Il est facile d'en trouver 2 points en remplaçant, par exemple, $x$ par 0 pour l'un, et $y$ par 0 pour l'autre.
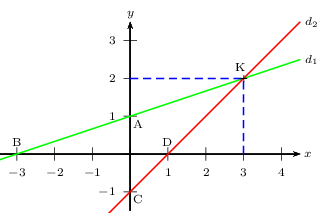
La première ligne est associée à la droite $d_1$ passant par les points $A(0;1)$ et $B(-3;0)$.
Ici, pour trouver A, on a écrit: $0-3y+3=0$, ce qui a donné: $y=1$.
Et pour trouver B, on a écrit: $x-3×0+3=0$, ce qui a donné: $x=-3$.
De même, la seconde ligne est associée à la droite $d_2$ passant par les points $C(0;-1)$ et $D(1;0)$.
D'où les tracés suivants:
Méthode 2: Cette méthode consiste à retrouver les équations réduites des droites associées à chaque ligne.
$\{\table x-3y+3=0; x-y-1=0$ $⇔$ $\{\table -3y=-x-3; -y=-x+1$ $⇔$ $\{\table y={1}/{3}x+1; y=x-1$
La droite $d_1$ d'équation $y={1}/{3}x+1$ passe par $A(0;1)$ et son coefficient directeur vaut ${1}/{3}$.
La droite $d_2$ d'équation $y=x-1$ passe par $C(0;-1)$ et son coefficient directeur vaut $1$.
On retrouve les tracés obtenus avec la première méthode.
2. Graphiquement, on constate que $d_1$ et $d_2$ se coupent au point K de coordonnées $(3;2)$.
Donc la solution du système est le couple $(x;y)=(3;2)$.
3.
Avec les notations usuelles, on a: $a=1$, $b=-3$, $a'=1$ et $b'=-1$.
On calcule: $ab'-a'b=1×(-1)-1×(-3)=2$. On a donc: $ab'-a'b≠0$.
Donc le système a bien une solution unique.
Résolution:
Méthode 1: Nous allons procéder par combinaisons linéaires.
Les combinaisons choisies (produit d'une ligne par un nombre non nul, somme ou soustraction de lignes) sont explicitées à droite des lignes concernées.
(S) $⇔$ $\{\table x-3y+3,=,0,(L_1); x-y-1,=,0,(L_2)$
$⇔$ $\{\table x-3y+3,=,0, (L_1); x-3y+3-x+y+1,=,0-0,(L_1-L_2 ⇨L_2)$
La soustraction $L_1-L_2 ⇨L_2$ permet d'éliminer l'inconnue $x$ dans la ligne $L_2$
(S) $⇔$ $\{\table x-3y+3,=,0,(L_1); -2y+4,=,0 ,(L_2)$
$⇔$ $\{\table x-3y+3,=,0; y,=,2$
$⇔$ $\{\table x-3×2+3,=,0 ; y,=,2 $
$⇔$ $\{\table x=3 ; y=2 $
Donc la solution du système est le couple $(x;y)=(3;2)$.
Méthode 2: Nous allons procéder par substitution.
(S) $⇔$ $\{\table y={-1}/{-3}x-{3}/{-3}; x-y-1=0$
Remplacer $y$ par son expression dans la seconde ligne permet d'éliminer l'inconnue $y$ dans dans la seconde ligne
$⇔$ $\{\table y={1}/{3}x+1; x-({1}/{3}x+1)-1=0$
$⇔$ $\{\table y={1}/{3}x+1; x-{1}/{3}x-1-1=0$
$⇔$ $\{\table y={1}/{3}x+1; {2}/{3}x=2$
$⇔$ $\{\table y={1}/{3}x+1; x=2×{3}/{2}=3$
$⇔$ $\{\table y={1}/{3}×3+1=2; x=3$
Donc la solution du système est le couple $(x;y)=(3;2)$.
Méthode 3: Pour les curieux, nous allons procéder par combinaisons linéaires en choisissant d'éliminer $y$ cette fois-ci.
(S) $⇔$ $\{\table x-3y+3,=,0,(L_1); x-y-1,=,0,(L_2)$
$⇔$ $\{\table x-3y+3,=,0, (L_1); 3x-3y-3,=,3×0,(3L_2 ⇨L_2)$
$⇔$ $\{\table x-3y+3,=,0, (L_1); x-3y+3-3x+3y+3,=,0-0,(L_1-L_2 ⇨L_2)$
La soustraction $L_1-L_2 ⇨L_2$ permet d'éliminer l'inconnue $y$ dans la ligne $L_2$
(S) $⇔$ $\{\table x-3y+3,=,0,(L_1); -2x+6,=,0 ,(L_2)$
$⇔$ $\{\table x-3y+3,=,0; x,=,3$
$⇔$ $\{\table 3-3y+3,=,0 ; x,=,3 $
$⇔$ $\{\table y=2 ; x=3 $
On retrouve la solution du système $(x;y)=(3;2)$.
Méthode 4: Pour les curieux, nous allons procéder par substitution en choisissant d'éliminer $x$ cette fois-ci.
(S) $⇔$ $\{\table x=3y-3; x-y-1=0$
Remplacer $x$ par son expression dans la seconde ligne permet d'éliminer l'inconnue $x$ dans dans la seconde ligne
$⇔$ $\{\table x=3y-3; x-y-1=0$
$⇔$ $\{\table x=3y-3; 3y-3-y-1=0$
$⇔$ $\{\table x=3y-3; 2y=4$
$⇔$ $\{\table x=3y-3; y=2$
$⇔$ $\{\table x=3×2-3=3; y=2$
Donc la solution du système est le couple $(x;y)=(3;2)$.