 Généralités sur les fonctions
Généralités sur les fonctions
I. Quelques définitions
Définition 1
Soit $\D$ une partie de $ℝ$.
On définit une fonction $f$ sur l'ensemble $\D$ lorsque l'on associe à chaque réel $x$ de $\D$ un unique réel $y$.
Théoriquement, on note: $\table f:, D\→ℝ; ,x ↦ y=f(x)$
Dans la pratique, quand il n'y a pas d'ambiguïté sur $\D$, on note simplement: $y=f(x)$.
Le nombre $f(x)$ s'appelle l'image de $x$ par $f$. Pour un $x$ donné, il n'existe qu'un seul $f(x)$.
Si $y=f(x)$, alors le nombre $x$ est un antécédent de $y$ par $f$. Pour un $y$ donné, il peut n'exister aucun $x$, ou exister un ou plusieurs $x$, tels que $y=f(x)$.
Exemple
Considérons la fonction: $\table f:,ℝ_{+}\→ℝ; ,x ↦ √ {x}-2$
A chaque réel $x$ positif ou nul, on associe le réel $f(x)= √ {x}-2$.
Quelle est l'image de 9 par $f$ ?
L'image de 9 par $f$ est 1, car $f(9)=√ {9}-2=3-2=1$
Donnons un antécédent de 1 par $f$.
Comme $f(9)=1$, un antécédent de 1 par $f$ est 9.
Montrons que 1 admet un seul antécédent par $f$.
Le nombre 1 admet un antécédent unique par $f$ (qui est 9), car l'équation $f(x)=1$ admet une unique solution (qui est 9).
En effet: $f(x)=1$ $⇔$ $√ {x}-2=1$ $⇔$ $√ {x}=1+2$ $⇔$ $√ {x}=3$ $⇔$ $x=3^2$ $⇔$ $x=9$
Définition 2
Dans le plan muni d'un repère, la courbe représentative de la fonction $f$ définie sur $\D$ est l'ensemble des points de coordonnées $(\ x\ ;\ f(x)\ )$
lorsque $x$ décrit l'ensemble $\D$.
On la note souvent: $\C_f$.
Dire que $\C_f$ a pour équation: $y=f(x)$, c'est dire que, pour tout nombre $x$ de $\D$,
si le point de coordonnées $(x,y)$ est sur $\C_f$, alors $y=f(x)$,
et si $y=f(x)$, alors le point de coordonnées $(x,y)$ est sur $\C_f$.
Exemple
Considérons la fonction: $\table f:, ℝ_{+} \→ℝ; ,x ↦ √ {x}-2$
Traçons sa courbe représentative $\C_f$ pour retrouver graphiquement les résultats obtenus dans l'exemple précédent.
Il suffit de dresser un tableau de valeurs pour obtenir les coordonnées de quelques points de $\C_f$.
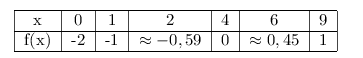
D'où le tracé qui suit.
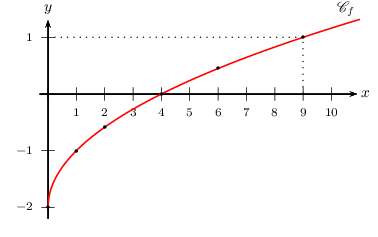
On constate graphiquement que l'image de 9 par $f$ est effectivement 1, et que 1 admet bien un seul antécédent par $f$, qui est évidemment 9.
Définition 3
Le domaine de définition d'une fonction $f$, souvent noté $\D_f$, est le plus grand ensemble de nombres réels $x$ tels que $f(x)$ existe.
Exemple
Considérons à nouveau la fonction $f$ définie par $f(x)=√ {x}-2$
Le domaine de définition de $f$ est $ℝ_{+}=[ 0 ; +\∞ [$ car, comme $√ {x}$ n'existe que lorsque $x$ est positif ou nul, il en est de même pour $f(x)$.
Définition 4
La fonction $f$ définie sur l'intervalle I est strictement croissante si et seulement si les images $f(x)$ sont de plus en plus grandes quand $x$ augmente.
$f$ est strictement croissante sur I $⇔$ pour tous $a$ et $b$ de I, si $a<b$, alors $f(a)<f(b)$.
Définition 4 bis
La fonction $f$ définie sur l'intervalle I est strictement décroissante si et seulement si les images $f(x)$ sont de plus en plus petites quand $x$ augmente.
$f$ est strictement décroissante sur I $⇔$ pour tous $a$ et $b$ de I, si $a<b$, alors $f(a)>f(b)$.
Définition 5
s'il existe, le maximum M d'une fonction $f$ définie sur un ensemble $\D$ est la plus grande des images $f(x)$ lorsque $x$ décrit $\D$.
M est le maximum de $f$ sur $\D$
$⇔$ il existe $c$ dans $\D$ tel que $f(c)=M$, et, pour tout $x$ de $\D$, $f(x)≤ M$
Définition 5 bis
s'il existe, le minimum $m$ d'une fonction $f$ définie sur un ensemble $\D$ est la plus petite des images $f(x)$ lorsque $x$ décrit $\D$.
$m$ est le minimum de $f$ sur $\D$
$⇔$ il existe $c$ dans $\D$ tel que $f(c)=m$, et, pour tout $x$ de $\D$, $f(x)≥ M$
Le sens de variation d'une fonction, ainsi que ses éventuels extrema, apparaissent dans un tableau de variation (voir exemple 4 du II).
Attention !
Ne pas confondre tableau de valeurs, tableau de signes et tableau de variation.
II. Quelques exemples
Exemple 1
L'aire d'un carré dépend de la longueur de ses côtés.
Déterminer la fonction $f$ donnant l'aire (en $cm^2$) d'un carré de côté non nul $x$ (en $cm$).
Corrigé
L'aire cherchée est donnée par la fonction: $f(x)=x^2$ définie sur $\D=$] $0$ ; $+\∞$ [
On note également: $\D={ℝ}^{*}_{+}$
Exemple 2
Pierre lance un dé et gagne une somme (en euros) qui dépend du résultat obtenu suivant le tableau suivant.

Sur quel ensemble $\D$ est définie la fonction $f$?
Quelle est l'image de 6 par $f$? Que cela signifie-t-il?
Corrigé
$f$ est définie sur $\D=\{1,2,3,4,5,6\}$
On notera que le tableau de valeurs est "complet" (il contient bien toutes les valeurs de $\D$).
L'image de 6 par $f$ est 100. On écrit aussi: $f(6)=100$
Cela signifie que, si le résultat du dé est 6, alors Pierre gagne 100 euros.
Exemple 3
Les âges $x$ (en années) et les tailles $y$ (en $cm$) des 12 enfants d'un village sont répertoriées dans le tableau ci-dessous:

Il est clair que la taille dépend de l'âge. Mais peut-on dire que la taille $y$ est une fonction de l'âge $x$ ?
Corrigé
La taille $y$ n'est pas une fonction de l'âge $x$.
En effet, chaque valeur de $x$ n'est pas associée à une unique "image" $y$.
Par exemple, pour $x=6$, il y a deux $y$ possibles qui sont 105 et 112.
Exemple 4
On introduit une substance S dans un liquide contenant un certain type de micro-organismes afin d'en stopper la prolifération.
Le nombre de micro-organismes varie en fonction du temps écoulé depuis l'introduction de la substance S.
Le nombre (en millions) de micro-organismes présents au bout du temps $x$ (en heures) écoulé depuis l'introduction de la substance S est donné par la fonction $f$ représentée ci-après.
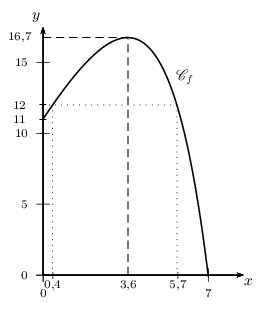
- Sur quel ensemble $\D$ est définie la fonction $f$?
- Quelle est l'image de 0,4 par $f$? Que cela signifie-t-il?
- Quelle est l'image de 5,7 par $f$? Que cela signifie-t-il?
- Quels sont les antécédents de 12 par $f$?
- Résoudre l'équation $f(x)=12$
- Dresser le tableau de variations de $f$ sur $[0;7]$
- A l'aide du tableau précédent, comparer $f(4)$ à $f(4,1)$
- Quel est le maximum M de $f$ sur $[0;7]$? Pour quel $x$ est-il atteint?
- Quel est le minimum $m$ de $f$ sur $[0;7]$? Pour quel $x$ est-il atteint?
Corrigé
-
La fonction $f$ est définie sur $\D=$[ $0$ ; $7$ ]
Eventuellement, on peut proposer que $f$ soit définie sur $\D=$[ $0$ ; $+\∞$ [ - L'image de 0,4 par $f$ est 12. On écrit aussi: $f(0,4)=12$
Cela signifie que, au bout de $0,4$ heures, le nombre de micro-organismes présents est de 12 millions.
Remarque: $0,4$ heures représentent 24 minutes. - L'image de 2,7 par $f$ est 12. On écrit aussi: $f(5,7)=12$
Cela signifie que, au bout de $5,7$ heures, le nombre de micro-organismes présents est de 12 millions.
Remarque: $5,7$ heures représentent 5 heures et 42 minutes. - Les antécédents de 12 par $f$ sont $0,4$ et $5,7$.
Remarque: noter l'utilisation de la conjonction "et" car on énumère les antécédents. - Chercher les antécédents de 12 par $f$ revient à résoudre l'équation $f(x)=12$.
Donc: $f(x)=12$ $⇔$ $ x=0,4$ ou $x=5,7$
Par conséquent, l'ensemble des solutions est: $\S=\{\,0,4\,;\,5,7\,\}$
Remarque: dans la résolution de l'équation, noter l'utilisation de la conjonction "ou" qui a un caractère logique. - Voici le tableau de variations de $f$ sur $[0;7]$
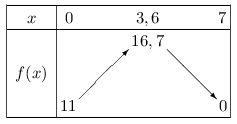
- On a: $4<4,1$.
Or, d'après le tableau précédent, $f$ est strictement décroissante entre 4 et 4,1.
Donc: $f(4)>f(4,1)$ - Le maximum de $f$ sur $[0;7]$ est $M=16,7$.
Il est atteint pour $x=3,6$ - Le minimum de $f$ sur $[0;7]$ est $m=0$.
Il est atteint pour $x=7$
Exemple 5
Déterminer le domaine de définition de $f$ définie par $f(x)={1}/{x-2}$
Corrigé
On rappelle qu'un quotient n'existe que si son dénominateur n'est pas nul.
On doit avoir: $x-2≠0$, c'est à dire: $x≠2$
Donc: $\D_f=$] $-\∞$ ; $2$ [$∪$] $2$ ; $+\∞$ [
On peut aussi écrire: $\D_f=ℝ\\\{2\}$
Exemple 6
Déterminer le domaine de définition de $g$ définie par $g(x)=√ {x-3}$
Corrigé
On rappelle que la racine carrée d'un nombre n'existe que si ce nombre est positif ou nul.
On doit avoir: $x-3≥$, c'est à dire: $x≥3$
Donc: $\D_g=$[ $3$ ; $+\∞$ [