 Nombres et calculs
Nombres et calculs
I. Les types de nombres
a. Les ensembles de nombres remarquables
Notation
Pour décrire certains ensembles, on peut écrire la liste de leurs éléments entre 2 accolades.
Exemple
L'ensemble des résultats d'un dé est: $\{ 1 ; 2 ; 3 ; 4 ; 5 ; 6 \}$
Rappel:
$10^0=1$ $10^1=10$
$10^2=10×10=100$ $10^3=10×10×10=1000$
Définitions
Les ensembles de nombres remarquables sont $ℕ$, $ℤ$, 𝔻, $ℚ$ et $ℝ$.
$ℕ$ est l'ensemble des entiers naturels. On a donc: $ℕ= \{ 0 ; 1 ; 2 ; 3 ; 4 ; ...\}$
$ℤ$ est l'ensemble des entiers relatifs. On a donc: $ℤ= \{ ... ; -4 ; -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; 3 ; 4 ; ...\}$
𝔻 est l'ensemble des nombres décimaux.
Les nombres décimaux sont les nombres qui s'écrivent comme quotient d'un entier par $10^k$, où $k$ est un entier naturel.
$ℚ$ est l'ensemble des nombres rationnels.
Les nombres rationnels sont les nombres qui s'écrivent comme quotient de 2 entiers relatifs.
$ℝ$ est l'ensemble des nombres réels.
Les nombres réels sont les abscisses de tous les points d'une droite graduée. Une telle droite s'appelle droite des réels.
Propriété
Les ensembles de nombres précédents sont inclus (contenus) les uns dans les autres.
$ℕ$ est inclus dans $ℤ$. $ℤ$ est inclus dans 𝔻. 𝔻 est inclus dans $ℚ$.
$ℚ$ est inclus dans $ℝ$.
On note: $ℕ⊂ℤ⊂$𝔻$⊂ℚ⊂ℝ$.
Représentation par un diagramme de Venn
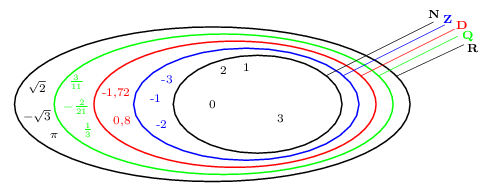
Exemple
$-1,72$ n'est évidemment ni un entier naturel, ni un entier relatif.
$-1,72$ est un nombre décimal car on peut écrire: $-1,72={-172}/{100}={-172}/{10^2}$
C'est donc également un rationnel, et aussi un réel.
Exemples de nombres réels
$0$ $1$ $-2,7$
${1}/{3}≈0,3333$ $√{2}≈1,4124$ $ π≈3,1416$
Ces nombres se placent sur la droite des réels ci-dessous.

b. La nature des nombres
Définition
La nature d'un nombre est liée au plus petit ensemble parmi $ℕ$, $ℤ$, 𝔻, $ℚ$ et $ℝ$ auquel il appartient.
Exemple
La nature de $2,18$ est d'être un décimal car il appartient à 𝔻, mais pas à $ℤ$.
Définition
Un irrationnel est un nombre réel qui n'est pas rationnel.
Par exemple, $√{2}$ et $π$ sont des irrationnels.
La nature d'un irrationnel est évidemment d'être un réel.
Exemple
Donner, sans justifier, la nature de chacun des nombres suivants:
$3$ $2,1$ ${1}/{3}$
$√{2}$ et $π$.
Corrigé
$3$ est un entier naturel.
$-2$ est un entier relatif (ce n'est pas un entier naturel).
$2,1$ est un décimal (ce n'est pas un entier relatif, et encore moins un entier naturel).
${1}/{3$ est un rationnel (ce n'est pas un décimal).
$√{2}$ et $π$ sont des réels (ce sont des irrationnels)
Propriété 1
Un nombre non entier est décimal si et seulement si il admet une écriture décimale limitée.
Propriété 2
Un nombre rationnel non nul écrit sous la forme d'une fraction irréductible d'entiers ${p}/{q}$ (avec $q$ entier naturel) n'est pas un nombre décimal si et seulement si la décomposition de $q$ en produit de nombres premiers ne peut pas s'écrire sous la forme $2^m×5^n$ (avec $m$ et $n$ entiers naturels).
Propriété 3
Un nombre rationnel n'est pas décimal si et seulement si il est impossible de l'écrire sous forme décimale avec un nombre fini de décimales.
Propriété 4
Si un entier naturel n'est pas un carré d'entier, alors sa racine carrée est un nombre irrationnel.
Propriété 5
Un nombre réel est irrationnel si et seulement si son développement décimal est infini et n'est pas périodique.
A retenir
La nature d'un nombre est évidente s'il s'agit d'un entier naturel ou d'un entier relatif.
Elle est facile à déterminer s'il s'agit d'un nombre décimal (par sa définition ou grâce à la propriété 1).
La nature d'un rationnel se conjecture à l'aide de la propriété 3, et se prouve à l'aide de la propriété 2.
La nature d'un irrationnel se conjecture à l'aide de la propriété 5.
Par contre, pour prouver qu'un réel est irrationnel, c'est moins évident, excepté si l'on peut appliquer la propriété 4.
Exemple
Montrons que $12,726$ est un décimal de 2 façons difféentes.
Méthode 1 (en utilisant la propriété 1): $12,726$, non entier, est un décimal car il admet une écriture décimale limitée.
Méthode 2 (en utilisant la définition d'un décimal): $12,726$ est un décimal car il peut s'écrire ${12\,726}/{10^3}$
Exemple
a. Le rationnel non nul ${7}/{26}$ est-il décimal?
b. Le rationnel non nul ${11}/{20}$ est-il décimal?
Corrigé
a. A la calculatrice, on obtient: ${7}/{26}≈0,2692307692$. L'écriture décimale semble illimitée. ${7}/{26}$ n'est sans doute pas un décimal.
Mais ce n'est pas certain! Démontrons que ${7}/{26}$ n'est pas décimal à l'aide de la propriété 3.
On a : ${7}/{26}={7}/{2×13}$.
La fraction est irréductible, mais, si l'on décompose 26 en produit de nombres premiers, on obtient $26=2×13$. Par conséquent, 26 ne peut pas s'écrire sous la forme $2^m×5^n$ (avec $m$ et $n$ entiers naturels).
Donc ${7}/{26}$ n'est pas décimal.
b. Démontrons que ${11}/{20}$ est décimal de 2 façons différentes.
Méthode 1.
${11}/{20}={11}/{2^2×5}={11×5}/{2^2×5×5}={55}/{(2×5)^2}={55}/{10^2}$.
Donc, par définition, ${11}/{20}$ est décimal.
Méthode 2.
On calcule: ${11}/{20}=0,55$. Le nombre n'est pas entier, et son écriture décimale est limitée. Donc ${11}/{20}$ est décimal.
La méthode 2 est la plus rapide!.
Exemple
Le nombre $√{14}$ est-il un irrationnel ?
Corrigé
A la calculatice, on obtient: $√{14}≈3,741657387$.
L'écriture décimale semble illimitée et non périodique.
On conjecture que le nombre $√{14}$ est irrationnel, mais on n'en est pas certain!
Démontrons le à l'aide de la propriété 5.
On a: $3^2<14<4^2$. Donc 14 est strictement compris entre 2 carrés d'entiers consécutifs. Donc 14 n'est pas un carré d'entiers. Donc $√{14}$ est un irrationnel.
II. Intervalles. Encadrements décimaux
Définition 1
Un intervalle réel est un ensemble de nombres délimité par deux nombres réels constituant une borne inférieure et une borne supérieure. Un intervalle contient tous les nombres réels compris entre ces deux bornes.
Soient $a$ et $b$ deux réels avec $a<b$.
L'ensemble des réels $x$ tels que $a≤ x≤ b$ est l'intervalle noté [ $a$ ; $b$ ]
L'ensemble des réels $x$ tels que $a< x< b$ est l'intervalle noté ] $a$ ; $b$ [
L'ensemble des réels $x$ tels que $a≤ x<b$ est l'intervalle noté [ $a$ ; $b$ [
L'ensemble des réels $x$ tels que $a< x≤ b$ est l'intervalle noté ] $a$ ; $b$ ]
L'ensemble des réels $x$ tels que $a≤ x$ est l'intervalle noté [ $a$ ; $+\∞$ [
L'ensemble des réels $x$ tels que $a< x$ est l'intervalle noté ] $a$ ; $+\∞$ [
L'ensemble des réels $x$ tels que $ x≤ b$ est l'intervalle noté ] $-\∞$ ; $b$ ]
L'ensemble des réels $x$ tels que $x < b$ est l'intervalle noté ] $-\∞$ ; $b$ [
Aux 8 types d'intervalles précédents s'ajoute l'intervalle particulier suivant:
l'ensemble vide, qui ne contient aucun nombre, et qui est noté $∅$
On notera les intervalles particuliers que sont:
les singletons du type $\{a\} =$ [ $a$ ; $a$ ]
l'ensemble des nombres réels $ℝ = ] -\∞$ ; $+ \∞ [$
Définition 2
Les 4 premiers types d'intervalles de la définition 1 ont pour longueur $b-a$.
Un singleton a une longueur nulle.
Définition 3
Soient I et J deux intervalles.
La réunion de I et de J, notée $I∪ J$, est l'ensemble des réels appartenant à I, ou à J, ou à I et à J à la fois.
L'intersection de I et de J, notée $I∩ J$, est l'ensemble des réels appartenant à I et à J à la fois.
Attention ! Ne pas confondre réunion et intersection ! L'intersection de deux ensembles doit être incluse dans leur réunion.
Exemple
Soit $I=[-1;3[$ et $J=]0;4]$.
Déterminer $I∪ J$ et $I∩ J$.
Corrigé
Le symbole $⇔$ signifie "équivaut à" ou "si et seulement si"
$x∈ I$ $⇔$ $-1≤ x<3$ (zone rouge sur le dessin ci-dessous)
$x∈ J$ $⇔$ $0< x≤ 4$ (zone bleue sur le dessin ci-dessous)

$x∈ I∪ J$ $⇔$ $-1≤ x<3$ ou $0< x≤ 4$ $⇔$ $-1≤ x≤ 4$
Donc: $I∪ J=[-1;4]$ (zone rouge ou bleue ou bicolore sur le dessin)
$x∈ I∩ J$ $⇔$ $-1≤ x<3$ et $0< x≤ 4$ $⇔$ $0< x<3$
Donc: $I∩ J=]0;3[$ (zone rouge et bleue sur le dessin)
Chacun peut vérifier que l'intersection de I et J est bien incluse dans leur réunion.
Les experts peuvent retenir les notations suivantes:
$[0;+∞[=ℝ_{+}$ et $]-∞;0]=ℝ_{-}$
$]0;+∞[=ℝ_{+}^{*}$ et $]-∞;0[=ℝ_{-}^{*}$ et $]-∞;0[∪]0;+∞[=ℝ^{*}$
Définition 4
Donner un encadrement décimal d'un réel $x$, c'est donner 2 nombres décimaux $a$ et $b$ tels que $a≤ x≤ b$.
Le nombre $b-a$ est appelé amplitude de l'encadrement.
Un encadrement est à $10^{-n}$ près (où $n$ est un entier) si son amplitude vaut $10^{-n}$.
Exemple
Donner un encadrement décimal d'amplitude $10^{-2}$ de $√{2}$ sachant que $√{2}≈1,414$
Corrigé
Un encadrement convenable est $1,41≤√{2}≤1,42$ car $1,42-1,41=0,01=10^{-2}$
La connaissance des intervalles est essentielle pour la résolution des inéquations!
III. Valeur absolue
Définition 1
Soient $a$ et $b$ deux réels.
La valeur absolue de $b-a$, notée $|b-a|$, est la distance entre les nombres $b$ et $a$ (sur la droite des réels).
Propriété 1
Pour tous réels $a$ et $b$, on a: $|b-a|=|a-b|$
Exemple
Déterminer $|2,5-1|$, $|1-4,2|$, $|2,5+1|$ et $|-2,5-1|$
Corrigé

$|2,5-1|=2,5-1=1,5$ (en rouge sur le dessin ci-dessus)
$|1-4,2|=|4,2-1|=4,2-1=3,2$ (en bleu sur le dessin ci-dessus)
$|2,5+1|=|2,5-(-1)|=2,5+1=3,5$ (en vert sur le dessin ci-dessus)
$|-2,5-1|=|1-(-2,5)|=1+2,5=3,5$ (en rose sur le dessin ci-dessus)
Propriété 2
Si $a$ est un nombre réel, alors $|a|$ est la distance entre $a$ et 0.
Si $a≥ 0$, alors $|a|=a$.
Si $a≤ 0$, alors $|a|=-a$.
Exemple
On a: $|7,3|=7,3$ $|-9,18|=-(-9,18)=9,18$ $|0|=0$
Propriété 3
Soit $a$ un réel quelconque et $r$ un réel strictement positif.
$x ∈ [a-r$ ; $a+r]$ $⇔$ $a-r≤ x≤ a+r$ $⇔$ $|x-a|≤ r$

Exemple
Ecrire avec une valeur absolue le fait que $x$ appartienne à l'intervalle [3;5]
Corrigé
L'astuce est de repérer le centre de l'intervalle! Ici, le centre est 4. Et la distance entre 4 et 3 (ou entre 4 et 5) vaut 1.
$x ∈ [3$ ; $5]$ $⇔$ $x ∈ [4-1$ ; $4+1]$ $⇔$ $4-1≤ x≤ 4+1$ $⇔$ $|x-4|≤ 1$
IV. Arithmétique
Définition 1
Soient $n$ et $m$ deux entiers relatifs.
$n$ est un multiple de $m$ si et seulement si il existe un entier relatif $k$ tel que $n=k× m$
Définition 2
Soient $n$ et $m$ deux entiers relatifs.
$m$ est un diviseur de $n$ si et seulement $n$ est un multiple de $m$
Propriété 1
Soient $n$ et $m$ deux entiers relatifs.
$m$ est un diviseur de $n$ si et seulement le reste de la division euclidienne de $n$ par $m$ vaut 0
Exemple
Appliquons les définitions 1 et 2 et la propriété 1 sur l'entier relatif $-12$.
Comme $-12=3×(-4)$, l'entier $-4$ est un diviseur de $-12$.
On peut aussi affirmer que $-12$ est un multiple de $-4$.
Et en utilisant l'écriture $-12=3×(-4)+0$, on constate que le reste de la division euclidienne de $-12$ par $-4$ vaut 0, ce qui confirme les affirmations précédentes.
En fait, les diviseurs de $-12$ sont: $-12$, $-6$, $-4$, $-3$, $-2$, -1$, 1, 2, 3, 4, 6 et 12.
Exemple
a. Montrer que la somme de 2 multiples d'un entier relatif $a$ est aussi un multiple de $a$.
b. Puis en déduire que la somme $87\,231+17\,565$ est un multiple de 3 sans calculer la somme donnée.
a. Les 2 multiples de $a$ peuvent s'écrire $ka$ pour l'un, et $k'a$ pour l'autre, où $k$ et $k'$ sont 2 entiers relatifs.
Leur somme vaut alors : $ka+k'a=(k+k')a$.
Et comme le facteur $k+k'$ est évidemment un entier relatif, la somme est donc effectivement un multiple de $a$.
b.
On calcule: $8+7+2+3+1=21$. Le résultat est divisible par 3. Donc le nombre $87\,231$ est divisible par 3.
On calcule: $1+7+5+6+5=24$. Le résultat est divisible par 3. Donc le nombre $17\,565$ est divisible par 3.
Comme $87\,231$ et $17\,565$ sont divisibles par 3, leur somme l'est aussi (d'après le a.).
Donc $87\,231+17\,565$ est un multiple de 3.
Définition 3
Un entier naturel $n$ est pair si et seulement si il existe un entier naturel $k$ tel que $n=2k$ (c'est un multiple de 2).
Un entier naturel $n$ est impair si et seulement si il existe un entier naturel $k$ tel que $n=2k+1$ (ce n'est pas un multiple de 2).
Propriété 2
Un entier naturel est soit pair, soit impair.
Exemple
Montrons que la somme $s$ de 2 entiers naturels impairs est paire.
Les 2 naturels impairs peuvent s'écrire $2k+1$ pour l'un et $2k'+1$ pour l'autre (avec $k$ et $k'$ entiers naturels).
Donc leur somme $s$ vérifie: $s=2k+1+2k'+1=2k+2k'+2=2(k+k'+1)$
Et comme $k+k'+1$ est évidemment un entier naturel, la somme $s$ est donc paire.
Exemple
a. Montrer que le carré d'un nombre naturel impair est un nombre impair.
b. Montrer sans calculatrice que $x=(2×731+1)^2-1$ est pair.
Corrigé
a. Un nombre impair peut s'écrire $2k+1$, où $k$ est un entier naturel.
Son carré s'écrit alors $(2k+1)^2=(2k)^2+2×2k×1+1^2=4k^2+4k+1=2(2k^2+2k)+1$
Et comme $2k^2+2k$ est évidemment un entier naturel, le carré est donc impair.
b. Par définition, $2×731+1$ est impair .
Donc: $(2×731+1)^2$ est impair également (d'après le a.).
Donc il existe un entier $k$ tel que $(2×731+1)^2=2k+1$ (par définition)
Et par là: $x=2k+1-1=2k$
Cela prouve que $x$ est pair (par définition).
Définition 4
Un entier naturel est un nombre premier si et seulement si il admet exactement 2 diviseurs positifs, 1 et lui même.
Propriété 3
Les 10 premiers nombres premiers sont: 2, 3, 5, 7, 11, 13, 17, 19, 23 et 29
Propriété 4
Soit $n$ un entier supérieur ou égal à 2.
Si aucun des nombres premiers inférieur ou égaux à $√{n}$ n'est un diviseur de $n$, alors $n$ est un nombre premier.
Exemple
Démontrer que 31 est un nombre premier.
Corrigé
31 est un entier supérieur ou égal à 2.
$√{31}≈5,6$.
Les nombres premiers inférieur ou égaux à $√{31}$ sont 2, 3 et 5.
Or aucun d'eux n'est un diviseur de 31.
Donc 31 est un nombre premier.
Propriété 5
Tout entier naturel supérieur ou égal à 2 s'écrit:
soit comme une puissance d'un nombre premier,
soit comme produit de puissances de nombres premiers.
Cette décomposition en produit de nombres premiers est unique, à l'ordre des facteurs près.
Exemples
$8=2^3$ $10=2×5$
$2268=2×1134=2×2×567=2^2×3×189=2^2×3×3×63=2^2×3^2×3×21=2^2×3^3×3×7=2^2×3^4×7$
Propriété 6
Tout rationnel admet une écriture sous forme de fraction irréductible, c'est à dire sous la forme ${p}/{q}$, où $p$ et $q$ sont deux entiers ayant pour seuls diviseurs communs $1$ et $-1$.
Cette écriture s'obtient facilement en décomposant numérateurs et dénominateurs en produits de nombres premiers.
Exemple
Sans calculatrice, écrire ${616}/{2268}$ sous forme irréductible.
Corrigé
Nous décomposons numérateurs et dénominateurs en produits de nombres premiers, puis on simplifie, si possible, la fraction obtenue.
On a: $616=2×308=2×2×154=2×2×2×77=2×2×2×7×11=2^3×7×11$
On a vu précédemment que: $2268=2^2×3^4×7$
Donc finalement: ${616}/{2268}={2^3×7×11}/{2^2×3^4×7}={2×11}/{3^4}={22}/{81}$
V. Calcul littéral
Propriété 1
Soient $a$ et $b$ deux réels (si besoin non nuls), et $m$ et $n$ deux entiers relatifs.
$a^m× a^n=a^{m+n}$ ${a^m}/{a^n}=a^{m-n}$ $(a^{m})^n=a^{m× n}$
$(a× b)^n=a^n× b^n$ $({a}/{b})^n={a^n}/{b^n}$
Définition 1
Soit $a$ un nombre réel positif.
Le nombre positif dont le carré est $a$ s'appelle la racine carrée de $a$ et se note $√{a}$.
Remarque: Si $a$ est un nombre réel positif, alors : $(√{a})^2=a$ (par définition)
Propriété 2
Soit $a$ un nombre réel quelconque. On a alors l'égalité: $√{a^2}=|a|$
Propriété 3
Pour tous nombres $a$ et $b$ positifs, on a: $√{a}×√{b}=√{a× b}$
Pour tout nombre $a$ positif et tout nombre $b$ strictement positif, on a: ${√{a}}/{√{b}}=√{{a}/{ b}}$
Pour tous nombres $a$ et $b$ strictement positifs, on a: $√{a}+√{b}>√{a+ b}$
Propriété 4
Soient $a$ et $b$ deux réels. On a alors les trois identités remarquables suivantes.
$(a+b)^2=a^2+2ab+b^2$ $(a-b)^2=a^2-2ab+b^2$ $(a-b)×(a+b)=a^2-b^2$
Le passage du membre de gauche à celui de droite est un développement.
Le passage du membre de droite à celui de gauche est une factorisation.
Définition 2
Factoriser consiste à écrire une somme algébrique sous forme d'un produit.
Développer consiste à écrire un produit algébrique sous forme d'une somme.
Exemple
Factoriser chacune des expressions suivantes.
$a(x)=x^2-6x$ $f(x)=x^2+6x+9$ $g(x)=9x^2-12x+4$ $h(x)=16x^2-6,25$
Corrigé
Pour $a(x)$, le facteur commun est évident; il s'agit de $x$, qui apparaît dans chacun des termes.
On a: $a(x)=x^2-6x=x×x-x×6=x×(x-6)$
Donc: $a(x)=x(x-6)$
Dans ce qui suit, le facteur commun n'est pas évident; il est donc onseillé d'utiliser, si possible, une identité remarquable.
Le nombre de termes et leurs signes permettent de choisir l'identité correcte.
On a: $f(x)=x^2+6x+9=x^2+2×x×3+3^2$
Donc: $f(x)=(x+3)^2$
On a: $g(x)=9x^2-12x+4=(3x)^2-2×3x×2+2^2$
Donc: $g(x)=(3x-2)^2$
On a: $h(x)=16x^2-6,25=(4x)^2-2,5^2$
Donc: $h(x)=(4x-2,5)(4x+2,5)$
Méthode pour factoriser (en seconde)
Chercher un facteur commun. S'il n'y en n'a pas, utiliser une identité remarquable.
Si rien ne fonctionne, c'est que la factorisation a été donnée auparavant !
Savoir factoriser est essentiel pour la résolution de certaines équations et inéquations.