 Orthogonalité
Orthogonalité
I. Trigonométrie et triangle rectangle
Définition
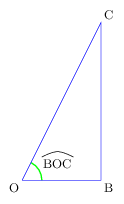
Si OBC est rectangle en B, alors:
$\cos O↖{∧}={OB}/{OC}={côté\,adjacent}/{hypoténuse}$
$\sin O↖{∧}={BC}/{OC}={côté\, opposé}/{hypoténuse}$ $\tan O↖{∧}={BC}/{OB}={côté\, opposé}/{côté\,adjacent}$
Propriété
Si OBC est rectangle en B, et si $α$ est un angle aigu de ce triangle, alors:
$0≤\cos α≤1$ $0≤\sin α≤1$
$\cos^2 α+\sin^2 α=1$
Et de plus: $\tan α={\sin α}/{\cos α}$
Notation:
$\cos (α)=\cos α$ $\cos^2 α=(\cos α)^2=(\cos α) ×(\cos α)$
$\sin (α)=\sin α$ $\sin^2 α=(\sin α)^2=(\sin α) ×(\sin α)$
$\tan (α)=\tan α$ $\tan^2 α=(\tan α)^2=(\tan α) ×(\tan α)$
Propriété
Quelques valeurs remarquables à connaître
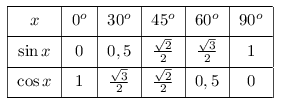
Exemple
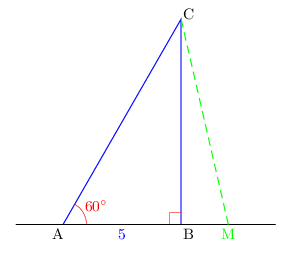
ABC est rectangle en B. $AB=5$. $A↖{∧}=60°$.
Déterminer BC et CA.
Corrigé
ABC est rectangle en B.
Donc: $\cos A↖{∧}={AB}/{AC}$
Soit: $\cos 60°={5}/{AC}$
Et donc: $AC={5}/{\cos 60°}$
Soit: $AC={5}/{0,5}=$$10$
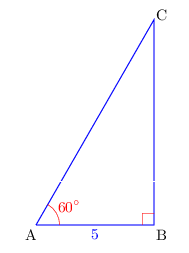
ABC est rectangle en B.
Donc, d'après le théorème de pythagore, on a: $AC^2=AB^2+BC^2$
Et par là: $BC^2=AC^2-AB^2=10^2-5^2=75$
Et donc, comme BC est positif, on obtient: $BC=√{75}=$$5√{3}$$≈8,7$
Autre méthode
ABC est rectangle en B.
Donc: $\sin A↖{∧}={BC}/{AC}$
Soit: $\sin 60°={BC}/{10}$
Et donc: $BC=10×\sin 60°$
Soit: $BC=10×{√{3}}/{2}=$$5√{3}$$≈8,7$
II. Projeté orthogonal d'un point sur une droite
Définition
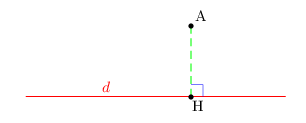
Soient A un point et $d$ une droite
Le projeté orthogonal de A sur $d$ est le point H de $d$ tel que (AH) est perpendiculaire à $d$
Propriété et définition
Soient A un point et $d$ une droite
Le projeté orthogonal H de A sur $d$ est le point de $d$ le plus proche de A.
La distance AH est appelée distance du point A à la droite $d$.
Exemple
On reprend le triangle ABC de l'exemple précédent. On rappelle que:
ABC est rectangle en B. $AB=5$. $A↖{∧}=60°$.
Par ailleurs: $AC=10$ $BC=5√{3}$
Soit M un point de la droite (AB). Comparer $CM$ à $5√{3}$.
Corrigé
ABC est rectangle en B.
Donc B est le projeté orthogonal de C sur la droite (AB).
Donc la distance entre C et la droite (AB) vaut CB, c'est à dire $5√{3}$.
Donc, comme M est sur (AB), on a: $CM≥5√{3}$.
Définition
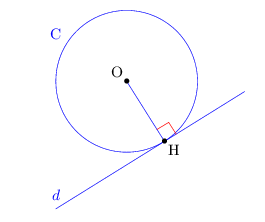
Soit $\C$ un cercle de centre O et H un point de $\C$.
Une droite $d$ est tangente à $\C$ en H lorsque $d$ passe par H et qu'elle est perpendiculaire à $(OH)$.
Exemple
Soit $\C$ un cercle de centre O et de rayon $r$.
- Montrer que, si $d$ est une droite tangente à $\C$ en un point H, alors la distance entre O et $d$ vaut $r$.
- Montrer que, si $d$ est une droite telle que la distance entre O et $d$ vaut $r$, alors $d$ est tangente à $\C$ en un point H.
- Soit M un point situé sur la tangente à $\C$ en H. Comparer $r$ et $OM$.
Corrigé
- $\C$ un cercle de centre O et de rayon $r$. Et $d$ est tangente à $\C$ en H.
Donc, d'une part: $OH=r$ (1),
et d'autre part, $d$ passe par H et elle est perpendiculaire à $(OH)$.
Donc H est le projeté orthogonal de O sur la droite $d$.
Donc, d'après (1), la distance entre O et $d$ vaut $OH=r$. -
Soit H le projeté orthogonal de O sur la droite $d$.
Donc H est sur $d$ et (OH) est perpendiculaire à $d$ (2).
Et, comme la distance entre O et $d$ vaut $r$, on a de plus: $OH=r$,
ce qui implique que H appartienne au cercle $\C$ de centre O et de rayon $r$.
Donc, d'après (2), $d$ est tangente à $\C$ au point H. -
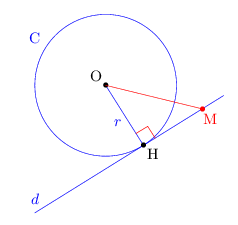
Comm M est sur la tangente $d$ à $\C$ en H, et que la distance entre O et $d$ vaut $r$, on a: $OM≥r$.