 Pourcentages
Pourcentages
Pourcentages simples
$t\,\,%$ d'un nombre s'obtient en multipliant le nombre par ${t}/{100}$
Exemple
Un objet vaut 110 euros hors taxes. La TVA (taxe sur la valeur ajoutée) s'élève à 6,05 euros.
Quel pourcentage du prix hors taxes représente la TVA?
Corrigé
Soit $t\,\,%$ la valeur cherchée.
Méthode 1
On a: ${t}/{100}×110=6,05$
Et donc: $t=6,05×{100}/{110}=5,5$
La TVA représente donc $5,5\,\,%$ du prix HT.
Méthode 2
On dresse le tableau de proportionnalité suivant
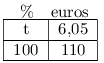
Et donc: $t={6,05×100}/{110}=5,5$
La TVA représente donc $5,5\,\,%$ du prix HT.
Pourcentages de pourcentages
Un pourcentage de pourcentage s'obtient en multipliant les pourcentages.
Exemple
$60\,\,%$ des élèves d'un lycée sont des filles.
$10\,\,%$ des filles du lycée pratiquent la danse.
Quel pourcentage des élèves du lycée représentent les filles du lycée qui pratiquent la danse?
Corrigé
On calcule: $10\,\,%×60\,\,%={10}/{100}×{60}/{100}={6}/{100}=0,06=6\,\,%$
Les filles du lycée qui pratiquent la danse représentent $6\,\,%$ des élèves du lycée.
Evolution en pourcentage
Soient $V_D$ et $V_A$ et $t$ trois nombres positifs.
$V_D$ augmenté de $t\,\,%$ devient $V_A$
si et seulement si
$V_A=V_D×(1+t\,\,%)$
$V_D$ diminué de $t\,\,%$ devient $V_A$
si et seulement si
$V_A=V_D×(1-t\,\,%)$
Exemple
Un objet est vendu 83,72 euros TTC (toutes taxes comprises).
La TVA représente $19,6\,\,%$ du prix HT (hors taxes).
Soit $p$ le prix HT. Que vaut $p$?
Corrigé
Méthode 1
On a: $p×(1+19,6\,\,%)=83,72$
Soit: $1,196p=83,72$
Et donc: $p={83,72}/{1,196}=70$
Le prix HT est de 70 euros.
Méthode 2
Comme la TVA représente $19,6\,\,%$ du prix HT, le prix TTC représente $119,6\,\,%$ du prix HT.
On dresse le tableau de proportionnalité suivant
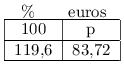
Et donc: $p={83,72×100}/{119,6}=70$
Le prix HT est de 70 euros.
Définition
Soit $t$ un réel strictement positif.
Si une grandeur strictement positive est augmentée de $t\,\,%$, alors $t\,\,%$ est appelé taux d'augmentation (ou pourcentage d'augmentation).
Le nombre $1+t\,\,%$ est appelé coefficient multiplicateur et il est strictement supérieur à 1.
Si une grandeur strictement positive est diminuée de $t\,\,%$, alors $t\,\,%$ est appelé taux de diminution (ou pourcentage de baisse).
Le nombre $1-t\,\,%$ est appelé coefficient multiplicateur et il est strictement inférieur à 1.
Le coefficient multiplicateur correspond à la valeur d'arrivée ($V_A$) lorsque la valeur de départ ($V_D$) vaut $100\,\,%=1$.
Propriété
Soient $V_D$ et $V_A$ et $t$ trois nombres positifs.
$t\,\,%$ est le taux d'évolution pour passer de $V_D$ à $V_A$.
En cas de hausse: $t\,\,%={V_A-V_D}/{V_D}$
En cas de baisse: $t\,\,%={V_D-V_A}/{V_D}$
Exemple 1
Le salaire d'un employé passe de 1450 euros par mois à 1529,75 euros par mois. Quelle est l'augmentation en pourcentage?
Corrigé
Soit $t\,\,%$ la hausse cherchée.
Méthode 1
On a: $t\,\,%={V_A-V_D}/{V_D}$
Soit: ${t}/{100}={1529,75-1450}/{1450}$
Soit: ${t}/{100}=0,055={5,5}/{100}$
Donc $t=5,5$
Et par là: $t\,\,%=5,5\,\,%$
Le salaire a augmenté de $5,5\,\,%$
Méthode 2
On a: $V_A=V_D×(1+t\,\,%)$
Soit: $1529,75=1450×(1+t\,\,%)$
Donc: ${1529,75}/{1450}=1+t\,\,%$
Soit: $1+t\,\,%=1,055=1+5,5\,\,%$
Et par là: $t\,\,%=5,5\,\,%$
Le salaire a augmenté de $5,5\,\,%$
Remarque: le coefficient multiplicateur de $1,055=105,5\,\,%$ correspond bien à une hausse de $5,5\,\,%$ (pour passer de $100\,\,%$ à $105,5\,\,%$)
Exemple 2
Le stock d'une entreprise subit une baisse de $t\,\,%$. Il passe de 250 kg à 200 kg. Que vaut $t$?
Corrigé
Méthode 1
On a: $t\,\,%={V_D-V_A}/{V_D}$
Soit: ${t}/{100}={250-200}/{250}$
Soit: ${t}/{100}=0,20={20}/{100}$
Donc $t=20$
Et par là: $t\,%=20\,%$
Le stock a baissé de $20\,%$
Méthode 2
On a: $V_A=V_D×(1-t\,%)$
Soit: $200=2450×(1-t\,%)$
Donc: ${200}/{250}=1-t\,%$
Soit: $1-t\,%=0,80=1-20\,%$
Et par là: $t=20$
Le stock a baissé de $20\,%$
Remarque: le coefficient multiplicateur de $0,80=80\,%$ correspond bien à une baisse de $20\,%$ (pour passer de $100\,%$ à $80\,%$)
Exemple 3
a. A quelle évolution correspond un coefficient multiplicateur égal à 1,196 ?
b. A quelle évolution correspond un coefficient multiplicateur égal à 0,84 ?
a. On a: $1,196=1+{19,6}/{100}$. Cela correspond à une hausse de $19,6\%$.
Autre méthode: le coefficient multiplicateur correspond à la valeur d'arrivée lorsque la valeur de départ vaut $100\,\,%$. Or $1,196=119,6\%$. Donc cela correspond à une hausse de $19,6\%$.
b. On a: $0,84=1-{16}/{100}$. Cela correspond à une baisse de $16\%$.
Autre méthode: le coefficient multiplicateur correspond à la valeur d'arrivée lorsque la valeur de départ vaut $100\,\,%$. Or $0,84=84\%$. Donc cela correspond à une baisse de $16\%$.
Définition
Soient $V_D$ et $V_A$ et $t$ trois nombres positifs.
Si $t\,%$ est le taux d'évolution pour passer de $V_D$ à $V_A$, alors le taux d'évolution réciproque est celui qui permet de passer de $V_A$ à $V_D$.
Exemple 1
Une action vient de baisser de $10\,%$. De quel pourcentage doit-elle remonter pour retrouver sa valeur initiale?
Corrigé
On cherche l''évolution réciproque d'une baisse de $10\,%$.
Méthode 1
Si $V_D$ est la valeur initiale de l'action, et $V_A$ sa valeur après la baisse, et si $t\,%$ est le pourcentage cherché, alors on a:
$V_A=V_D×(1-10\,%)$ et $V_D=V_A×(1+t\,%)$
Donc: $V_A=V_A×(1+t\,%)×(1-10\,%)$
Et, en divisant chaque membre par $V_A$ (non nul), on obtient:
$1=(1+t\,%)×(1-10\,%)$
Et donc: $1+t\,%={1}/{1-10\,%}≈1,111$
L'action doit remonter d'environ $11,1\,%$ pour retrouver sa valeur initiale.
Méthode 2
On cherche la hausse permettant de passer de $90\,%$ à $100\,%$
On calcule donc: ${V_A-V_D}/{V_D}={100-90}/{90}≈0,111$
Et comme $0,111={11,1}/{100}=11,1\,%$, on en déduit que l'action doit remonter d'environ $11,1\,%$ pour retrouver sa valeur initiale.
Exemple 2
Déterminer l'évolution réciproque d'une hausse de $10\,%$.
Corrigé
Méthode 1
Comme dans l'exemple précédent, si $t\,%$ est le pourcentage cherché, alors on obtient:
$1=(1-t\,%)×(1+10\,%)$
Et donc: $1-t\,%={1}/{1+10\,%}≈0,909$
Et comme $0,909=1-9,1\,%$, on en déduit que l'évolution réciproque d'une hausse de $10\,%$ est une baisse d'environ $9,1\,%$.
Méthode 2
On cherche la baisse permettant de passer de $110\,%$ à $100\,%$
On calcule donc: ${V_D-V_A}/{V_D}={110-100}/{110}≈0,091$
Et comme $0,091={9,1}/{100}=9,1\,%$, on en déduit que l'évolution réciproque d'une hausse de $10\,%$ est une baisse d'environ $9,1\,%$.
Evolutions successives
Le coefficient multiplicateur correspondant à plusieurs évolutions successives est égal au produit des coefficients multiplicateurs des évolutions successives.
Exemple 1
La population d'une ville augmente de $5\,%$ la première année, puis de $10\,%$ la seconde année.
a. Quelle est le pourcentage de hausse sur les 2 années?
b. Quelle est la "hausse moyenne" par année?
Corrigé
a. Les coefficients multiplicateurs successifs sont: $1+5\,%=1,05$ et $1+10\,%=1,10$.
Leur produit vaut alors: $1,05×1,10=1,155$
Et comme $1,155=1+15,5\,%$, cela correspond à une hausse totale de $15,5\,%$.
La population de la ville a augmenté de $15,5\,%$ sur 2 ans.
Attention, il ne faut pas sommer les pourcentages car ils ne se réfèrent pas à la même valeur!
Une autre méthode consiste à supposer que l'on part d'une valeur de départ fictive égale à $100\%$. Après les 2 hausses, elle est devenue égale à $115,5\%$. D'où la hausse totale de $15,5\%$ sur 2 ans.
b. On cherche la valeur de $t$ telle que deux hausses de $t\,%$ donnent une hausse de $15,5\,%$.
Les coefficients multiplicateurs successifs sont: $1+t\,%$ et $1+t\,%$.
Leur produit vaut alors: $(1+t\,%)^2=1,155$ car il correspond à une hausse totale de $15,5\,%$.
On résout donc l'équation (E): $(1+t\,%)^2=1,155$
(E) $⇔$ $1+t\,%=√{1,155}≈1,0747$ ou $1+t\,%=-√{1,155}≈-1,0747$ (ce qui est exclu car un coefficient multiplicateur de hausse est positif)
Donc: (E) $⇔$ $1+t\,%≈1,0747$ $⇔$ $t≈7,47$
La "hausse moyenne" est de $7,47\,%$ par mois.
Attention, il ne faut pas faire la moyenne des pourcentages car ils ne se réfèrent pas à la même valeur!
Exemple 2
Le prix d'un article est fixé au premier janvier.
Le prix augmente une première fois à la fin du mois de janvier, puis il augmente à nouveau un mois après. Cela correspond à une hausse totale de $44\,%$.
Quelle est la "hausse moyenne" par mois sur les deux mois de janvier et février?
Pour information, on cherche la valeur de $t$ telle que deux hausses de $t\,%$ donnent une hausse de $44\,%$.
Corrigé
Les coefficients multiplicateurs successifs sont: $1+t\,%$ et $1+t\,%$.
Leur produit vaut alors: $(1+t\,%)^2=1,44$ car il correspond à une hausse totale de $44\,%$.
On résout donc l'équation (E): $(1+t\,%)^2=1,44$
(E) $⇔$ $1+t\,%=√{1,44}=1,20$ ou $1+t\,%=-√{1,44}=-1,20$ (ce qui est exclu car un coefficient multiplicateur de hausse est positif)
Donc: (E) $⇔$ $1+t\,%=1,20$ $⇔$ $t=20$
La "hausse moyenne" est de $20\,%$ par mois.
A retenir
Les coefficients multiplicateurs, les taux d'évolution réciproques ou d'évolutions successives sont faciles à déterminer si l'on part d'une valeur de départ égale à $100\,%$.