 Les autres fonctions de référence
Les autres fonctions de référence
I. La fonction inverse $f(x)={1}/{x}$
Propriété 1
La fonction inverse est définie sur $]-\∞;0[∪]0;+\∞[=\ℝ\\\{0\}={\ℝ}^{*}$
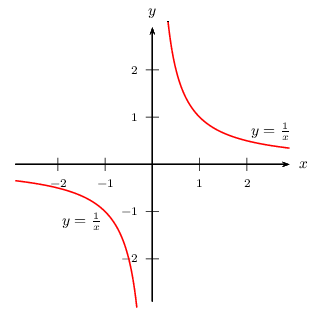
Elle est représentée par une hyperbole.
Cette hyperbole a pour centre de symétrie l'origine du repère.
En effet, pour tout nombre $x$, on a: $f(-x)=-f(x)$.
On dit que la fonction est impaire.
Tableau de valeurs et représentation graphique

Le X signifie que 0 n'a pas d'image.
Propriété 2
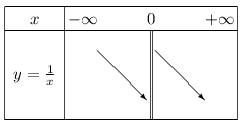
La fonction inverse admet le tableau de variation suivant.
Exemple 1
On suppose que $2< x< 3$ et $-5< t< -4$.
Encadrer ${1}/{x}$ et ${1}/{t}$.
Corrigé
On a: $2< x< 3$
Donc: ${1}/{2}> {1}/{x}> {1}/{3}$ ( car la fonction inverse est strictement décroissante sur ] $0$ ; $+\∞$ [ )
On a: $-5< t< -4$
Donc: ${1}/{-5}> {1}/{t}>{1}/{-4}$ ( car la fonction inverse est strictement décroissante sur ] $-\∞$ ; $0$ [] )
Propriété 3
La fonction inverse admet le tableau de signes suivant
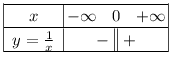
On notera qu'un nombre et son inverse ont même signe.
Equations et inéquations
Les équations et inéquations de référence concernant la fonction inverse sont du type:
${1}/{x}=k$ , ${1}/{x}<k$ , ${1}/{x}≤k$ ,
${1}/{x}>k$ et ${1}/{x}≥k$ (où $k$ est un réel fixé).
Elles se résolvent facilement si l'on connaît l'allure de l'hyperbole représentant la fonction inverse (voir l'exemple 2).
La maîtrise de ces équations et inéquations permet de résoudre les équations ou inéquation du type:
${1}/{f(x)}=k$ et ${1}/{f(x)}<k$ et celles obtenues en remplaçant $<$ par $≤$ ou $>$ ou $≥$
(où $k$ est un réel fixé et $f$ une fonction "simple" ) (voir l'exemple 3).
Exemple 2
- Résoudre l'équation ${1}/{x}=0,7$
- Résoudre l'inéquation ${1}/{x}≤0,7$
- Résoudre l'inéquation ${1}/{x}≥0,7$
Corrigé
- $\D_E=\ℝ\\\{0\}$
$0$ est une valeur "interdite". Ce ne peut pas être une solution.
Résolution.
${1}/{x}=0,7$ $⇔$ $x={1}/{0,7}$ Donc: S$=\{{1}/{0,7}\}$
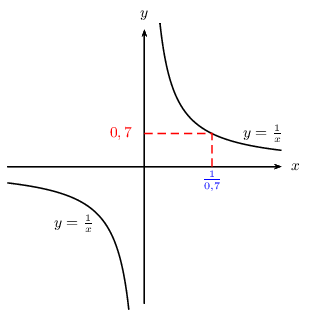
A retenir: si $a≠0$, alors: ${1}/{x}=a$ $⇔$ $x={1}/{a}$. - $\D_E=\ℝ\\\{0\}$
${1}/{x}≤0,7$ $⇔$ $x<0$ ou $x≥{1}/{0,7}$ Donc: S$=]-\∞;0$$[∪[$${1}/{0,7};+\∞[$
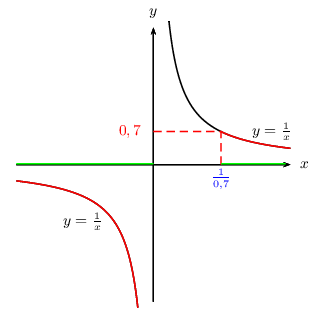
- $\D_E=\ℝ\\\{0\}$
${1}/{x}≥0,7$ $⇔$ $0<x≤{1}/{0,7}$ Donc: S$=]0;{1}/{0,7}$]
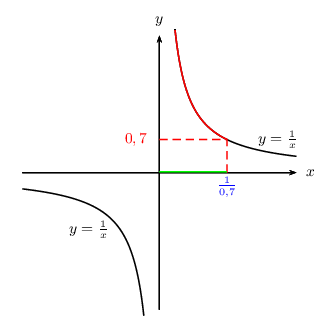
Exemple 3
Résoudre l'équation ${1}/{2x+1}-{2}/{5}=0$
Corrigé
On doit avoir: $2x+1≠0$. Soit: $x≠-{1}/{2}$
Donc le domaine d'étude est $\D_E=\ℝ\\\{-{1}/{2}\}$
Cela signifie que $-{1}/{2}$ est une valeur "interdite". Ce ne peut pas être une solution.
Résolution.
On commence par transposer $-{2}/{5}$ pour obtenir une équation du type ${1}/{f(x)}=k$.
${1}/{2x+1}-{2}/{5}=0$ $⇔$ ${1}/{2x+1}={2}/{5}$
$⇔$ $2x+1={5}/{2}$
$⇔$ $2x={5}/{2}-1$
$⇔$ $x={3}/{2}×{1}/{2}={3}/{4}$
S$=\{{3}/{4}\}$
On a bien entendu vérifié que ${3}/{4}$ n'est pas une valeur "interdite".
II. La fonction racine carrée $f(x)=√{x}$
Propriété 1
La fonction racine carrée est définie sur $[0;+\∞[={ℝ}_{+}$.
Dans un repère orthogonal, elle est représentée par une demi-parabole, dont le "sommet" est l'origine du repère.
La parabole associée aurait pour axe de symétrie l'axe des abscisses.
Tableau de valeurs et représentation graphique

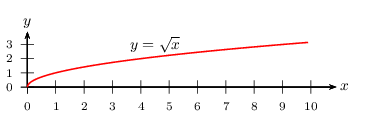
Propriété 2
La fonction racine carrée admet le tableau de variation suivant.
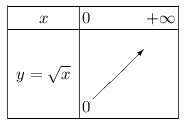
Exemple 1
On suppose que $2< x< 3$.
Encadrer $√{x}$.
Corrigé
On a: $2< x< 3$
Donc: $√{2}< √{x}< √{3}$ ( car la fonction racine carrée est strictement croissante sur [ $0$ ; $+\∞$ [ )
Propriété 3
La fonction racine carrée admet le tableau de signes suivant.
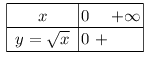
On notera que la racine carrée d'un nombre est toujours positive (ou nulle).
Equations et inéquations
Les équations et inéquations de référence concernant la fonction racine carrée sont du type:
$√{x}=k$ , $√{x}<k$ , $√{x}≤k$ ,
$√{x}>k$ et $√{x}≥k$ (où $k$ est un réel fixé).
Elles se résolvent facilement si l'on connaît l'allure de la demi-parabole représentant la fonction racine carrée (voir l'exemple 2).
La maîtrise de ces équations et inéquations permet de résoudre les équations ou inéquation du type:
$√{f(x}=k$ et $√{f(x}<k$ et celles obtenues en remplaçant $<$ par $≤$ ou $>$ ou $≥$ (où $k$ est un réel fixé et $f$ une fonction "simple") (voir l'exemple 3).
Exemple 2
- Résoudre l'équation $√{x}=10$
- Résoudre l'inéquation $√{x}≤10$
- Résoudre l'inéquation $√{x}≥10$
Corrigé
- $\D_E={ℝ}_{+}$
$√{x}=10$ $⇔$ $x=10^2=100$
S$=\{100\}$
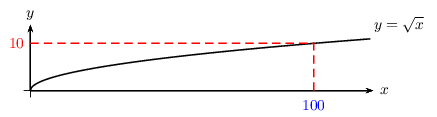
A retenir: si $a≥0$, alors: $√{x}=a$ $⇔$ $x=a^2$. - $\D_E={ℝ}_{+}$
$√{x}≤10$ $⇔$ $0≤x≤10^2$
S$=\[0;100\]$
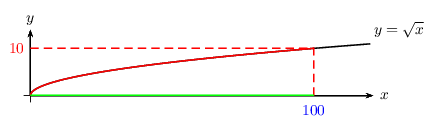
A retenir: si $a≥0$, alors: $√{x}≤a$ $⇔$ $0≤x≤a^2$. - $\D_E={ℝ}_{+}$
$√{x}≥10$ $⇔$ $10^2≤x$
S$=[100;+\∞[$
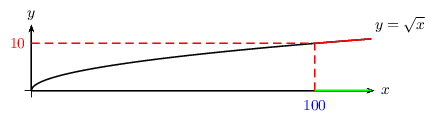
A retenir: si $a≥0$, alors: $√{x}≥a$ $⇔$ $x≥a^2$.
Exemple 3
Résoudre l'équation (E): $√{2x+1}-9=0$
Corrigé
On doit avoir: $2x+1≥0$. Soit: $x≥-{1}/{2}$
Donc le domaine d'étude est $\D_E=[-{1}/{2};+\∞[$
Cela signifie que les valeurs strictement inférieures à $-{1}/{2}$ sont "interdites".
Résolution.
On commence par transposer $-9$ pour obtenir une équation du type $√{f(x}=k$.
(E) $⇔$ $√{2x+1}=9$
$⇔$ $2x+1=9^2$
$⇔$ $x={81-1}/{2}=40$
S$=\{40\}$
On a bien entendu vérifié que $40$ n'est pas une valeur "interdite".
III. La fonction cube $f(x)=x^3$
Propriété 1
La fonction cube est définie sur $\ℝ$.
Elle est représentée par une cubique.
Cette cubique a pour centre de symétrie l'origine.
En effet, pour tout nombre $x$, on a: $f(-x)=-f(x)$.
On dit que la fonction est impaire.
Tableau de valeurs et représentation graphique
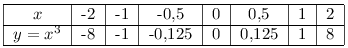
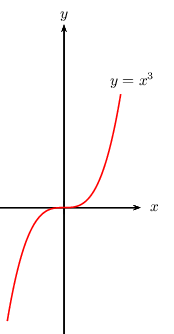
Propriété 2
La fonction cube admet le tableau de variation suivant.
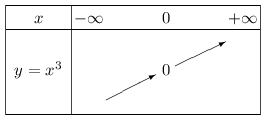
Exemple 1
On suppose que $-2< x< 3$.
Encadrer $x^3$.
Corrigé
On a: $-2< x< 3$
Donc: $(-2)^3< x^3< 3^3$ ( car la fonction cube est strictement croissante sur $\ℝ$ )
Soit: $-8< x^3< 27$
Propriété 3
La fonction cube admet le tableau de signes suivant.
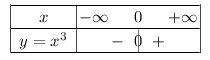
On notera qu'un nombre et son cube ont même signe.
Equations et inéquations
Les équations et inéquations de référence concernant la fonction cube sont du type:
$x^3=k^3$ , $x^3<k^3$ et celles obtenues en remplaçant $<$ par $≤$ ou $>$ ou $≥$ (où $k$ est un réel fixé).
Elles se résolvent facilement si l'on connaît l'allure de la cubique représentant la fonction cube (voir l'exemple 2).
La maîtrise de ces équations et inéquations permet de résoudre les équations ou inéquation du type:
$(f(x))^3=k^3$ et $(f(x))^3<k^3$ et celles obtenues en remplaçant $<$ par $≤$ ou $>$ ou $≥$ (où $k$ est un réel fixé et $f$ une fonction "simple") (voir l'exemple 3).
Exemple 2
- Résoudre l'équation $x^3=5^3$
- Résoudre l'inéquation $x^3≤5^3$
- Résoudre l'inéquation $x^3≥5^3$
Corrigé
-
$x^3=5^3$ $⇔$ $x=5$
S$=\{5\}$
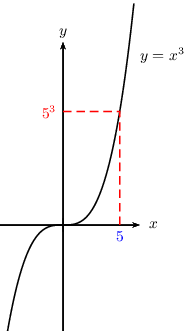
A retenir: $x^3=k^3$ $⇔$ $x=k$. -
$x^5≤5^3$ $⇔$ $x≤5$
S$=]-\∞;5]$
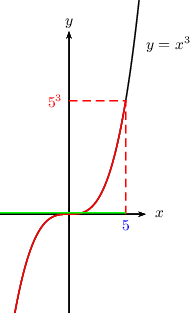
A retenir: $x^3≤k^3$ $⇔$ $x≤k$. -
$x^3≥5^3$ $⇔$ $x≥5$
S$=[5;+\∞[$
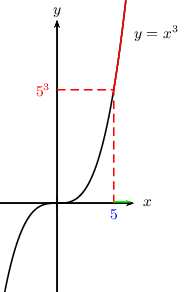
A retenir: $x^3≥k^3$ $⇔$ $x≥k$.
Exemple 3
Résoudre l'équation $(2x+1)^3=27$
Corrigé
$(2x+1)^3=27$ $⇔$ $(2x+1)^3=3^3$ $⇔$ $2x+1=3$
$⇔$ $2x=3-1$
$⇔$ $x={2}/{2}=1$
S$=\{1\}$