 Statistiques
Statistiques
I. Paramètres de position
Définitions
L'ensemble sur lequel porte l'étude d'une série statistique s'appelle la population. Un élément de la population est un individu. Une variable (ou un caractère) est une information dont on recueille (ou observe ou mesure) la valeur sur chaque individu.
Une série est qualitative lorsque le caractère étudié n'est pas numérique; sinon, la série est quantitative.
Une série quantitative est discrète lorsqu'elle prend des valeurs isolées.
Une série quantitative est continue lorsque ses valeurs sont regroupées dans des intervalles (ou classes).
L'effectif d'une valeur (ou d'une classe) est le nombre d’individus associés à la valeur (ou à la classe).
La fréquence d'une valeur (ou d'une classe) est le quotient de son effectif par l'effectif total.
L'effectif cumulé croissant d'une valeur est égal à la somme de l'effectif de cette valeur et des effectifs des valeurs qui lui sont inférieures.
La fréquence cumulée croissante d'une valeur est égal à la somme de la fréquence de cette valeur et des fréquences des valeurs qui lui sont inférieures.
 Exemple
Exemple
On considère les 3 séries suivantes, toutes 3 relatives à une classe de 22 élèves.
La première concerne la langue étudiée par chaque élève. Aucun élève n'étudie plus d'une langue.

La seconde série donne les notes obtenues lors du dernier devoir de maths.

La troisième série répertorie les tailles (en mètre) des élèves.

- Donner la nature de chacune des 3 séries.
- Représenter la série 1 par un diagramme en barres, puis par un diagramme circulaire.
- Représenter la série 2 par un diagramme en bâtons.
- Représenter la série 3 par un histogramme (pour lequel les aires des rectangles sont proportionnelles aux effectifs).
-
Déterminer les distributions des fréquences des série 2 et 3 (on donnera des valeurs approchées à $0,1%$ près).
Expliquer à quoi correspond la fréquence de $9,1%$ concernant la série 3. -
Dresser le tableau des fréquences cumulées croissantes de la série 3 (on donnera des valeurs approchées à $0,1%$ près).
Expliquer à quoi correspond la valeur de $72,8%$ du tableau.
Corrigé
- La série 1 est qualitative. La série 2 est quantitative discrète. La série 3 est quantitative continue.
-
La série 1 est représentée par ce diagramme en barres.

La série 1 est représentée par ce diagramme circulaire.
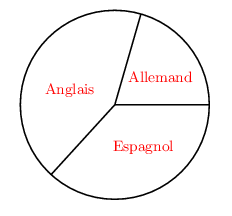
Les angles sont proportionnels aux effectifs avec le coefficient de proportionnalité ${360}/{22}≈16.36$ -
La série 2 est représentée par ce diagramme en bâtons.
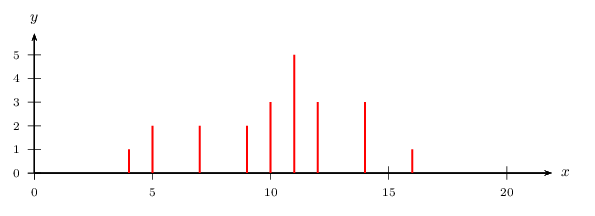
-
La série 3 est représentée par cet histogramme (pour lequel les aires des rectangles sont proportionnelles aux effectifs).
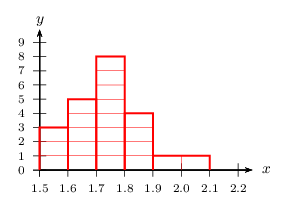
Attention! Les hauteurs des rectangles sont trompeuses. L'important, c'est leurs aires. Sur ce dessin, chaque élève est associé à un "petit rectangle". Il suffit de compter ces "petits rectangles" pour retrouver les effectifs. -
Voici les distributions des fréquences des série 2 et 3.

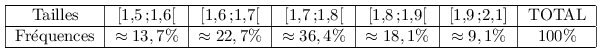
Les valeurs sont approchées à $0,1%$ près de façon à ce que leur somme fasse bien $100%$.
Par exemple, la fréquence de $9,1%$ est celle de la classe [1,90;2,10]. Environ $9,1%$ des élèves mesurent entre 1,90 m et 2,10 m. -
Voici le tableau des fréquences cumulées de la série 3.

Par exemple, on a calculé: $13,7+22,7+36,4=72,8%$. Environ $72,8%$ des élèves mesurent moins de 1,80 m.
Définitions
On considère une série statisque à une variable.
Si la série est discrète, ses valeurs sont désignées par les lettres $x_1$, $x_2$, ...$x_p$.
Si la série est continue, les $x_i$ désigne alors les centres des intervalles (cette simplification est convenable si la répartition des valeurs est uniforme dans chaque intervalle )
Les effectifs respectifs sont désignés par les lettres $n_1$, $n_2$, ...$n_p$.
Les fréquences respectives sont désignées par les lettres $f_1$, $f_2$, ...$f_p$.
L'effectif total de la série est $N=n_1+n_2+...+n_p$.
La moyenne de cette série, notée $x↖{−}$, vérifie:
$x↖{−}={n_1x_1+n_2x_2+...n_px_p}/{N}$
On a aussi: $x↖{−}=f_1x_1+f_2x_2+...+f_px_p$
 Exemple
Exemple
Déterminer la moyenne de chacune des séries 2 et 3.
Solution...Corrigé
Pour la série 2, on obtient:
$x↖{−}={1×4+2×5+2×7+2×9+3×10+5×11+3×12+3×14+1×16}/{1+2+2+3+5+3+3+1}={225}/{22}≈10,23$
La moyenne de classe du devoir est d'environ 10,23.
On aurait pu aussi faire le calcul suivant:
$x↖{−}={0,046×4+0,091×5+0,091×7+0,091×9+0,136×10+0,227×11+0,136×12+0,136×14+0,046×16≈10,22$
Pour la série 3, on obtient:
$x↖{−}={3×1,55+5×1,65+8×1,75+4×1,85+2×2,00}/{3+5+8+4+2}={34,8}/{22}≈1,74$
La taille moyenne des élèves de la classe est d'environ 1,74 m.
Propriété de linéarité
Soient $a$ et $b$ deux réels fixés.
Si la série $(x_i,n_i)$ ${\,}_{pour\, i\, allant\, de\, 1\, à\, p}$ a pour moyenne $x↖{−}$,
alors la série $(ax_i+b,n_i)$ ${\,}_{pour\, i\, allant\, de\, 1\, à\, p}$ a pour moyenne $ax↖{−}+b$
 Exemple
Exemple
Considérons le devoir de la série 2. Imaginons que le professeur décide d'augmenter chaque note de 10%, puis de rajouter 1 point à chaque élève.
Quelle serait la nouvelle moyenne de classe?
Corrigé
Le professeur multiplierait chaque note par 1,1, puis il lui ajouterait 1.
Par linéarité, la nouvelle moyenne de classe serait environ égale à:
$1,10x↖{−}+1=1,10×10,23+1≈12,25$
Définition
La médiane d'une série discrète ordonnée, souvent notée $m$, est la valeur centrale de la série si l'effectif total est impair, ou la moyenne de ses deux valeurs centrales si l'effectif total est pair.
La médiane d'une série continue est la valeur associée à une fréquence cumulée de $50\%$.
La médiane d'une série la partage en deux parties d'effectifs égaux (ou presque).
 Exemple
Exemple
Déterminer la médiane $m$ de la série 2.
Dresser le polygone des fréquences cumulées croissantes de la série 3, puis estimer graphiquement la médiane de cette série.
Corrigé
Série 2
Cette série a pour effectif total 22. Donc la médiane $m$ sera la moyenne de la 11ème valeur et de la 12éme valeur de la série ordonnée.
Or ces 2 valeurs valent 11. Cela se lit dans le tableau des valeurs, ou sur le gigrame en bâtons.
Donc $m={11+11}/{2}=11$
Voici le polygone des fréquences cumulées croissantes de la série 3.
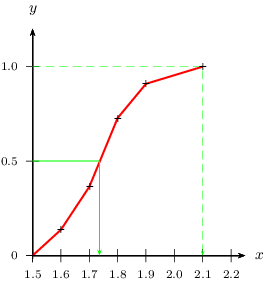
On note que, pr exemple, $100%$ des élèves mesurent au plus 2,10 m, et que $0%$ des élèves mesurent moins de 1,50 m.
La médiane de cette série continue est la valeur associée à une fréquence cumulée de $50\%$. Graphiquement, la médiane vaut environ 1,74 mètre.
On peut donc estimer que la moitié des élèves mesurent moins de 1,74 m.
Moyenne et médiane s'obtiennent à l'aide de la plupart des calculatrices en mode STATS.
II. Paramètres de dispersion
Définition
L'écart-type d'une série mesure la dispersion des valeurs de la série autour de sa moyenne. On le note souvent $s$ ou $σ$.
On l'obtient à l'aide de la calculatrice en mode STATS (où il est noté $σ_x$ ou $σ_n$ ou $σ$).
Pour les curieux, on a: $σ=√{{n_1(x_1-x↖{−})^2+n_2(x_2-x↖{−})^2+...+n_p(x_p-x↖{−})^2}/{N}}=√{{n_1{x_1}^2+n_2{x_2}^2+...+n_p{x_p}^2}/{N}-{x↖{−}}^2}$
Définitions et propriétés
Les quartiles d'une série ordonnée la partagent en 4 parties de mêmes effectifs (ou presque). Ils se notent $Q_1$, $Q_2$, $Q_3$ et $Q_4$.
$Q_1$ est la plus petite valeur de la série ordonnée telle que au moins $25\%$ des valeurs lui soient inférieures ou égales.
Les autres quartiles sont définis de façon similaire avec $50\%$, $75\%$ et $100\%$.
$Q_4$ est la plus grande valeur de la série. Médiane et $Q_2$ sont égaux (ou proches).
Environ $50\%$ des valeurs de la série sont comprises entre $Q_1$ et $Q_3$.
L'écart interquartile d'une série, souvent noté $EI$, vérifie: $EI=Q_3-Q_1$.
Il mesure la dispersion des valeurs de la série autour de sa médiane.
Propriété
Le couple ($x↖{−}$ ; $σ$) est sensible aux valeurs extrêmes de la série.
Le couple ($m$ ; $EI$) n'est pas sensible aux valeurs extrêmes de la série.
L'écart-type $σ$ et les quartiles $Q_1$ et $Q_3$ s'obtiennent à l'aide de la plupart des calculatrices en mode STATS.
 Exemple
Exemple
Déterminer l'écart-type $σ$ et l'écart interquartile $EI$ de la seconde série.

Le professeur décide de remonter quelques notes faibles; l'élève ayant eu 4 a finalement 7, les élèves ayant eu 5 ont finalement 8, et les élèves ayant eu 7 ont finalement 9.
Donner la nouvelle moyenne et le nouvel écart-type.
Qu'en dire?
La médiane et l'écart interquartile ont-il changés?
Corrigé
A la calculatrice, on obtient: $σ≈3,06$.
Déterminons $Q_1$ et $Q_3$.
On calcule ${25}/{100}×22=5,5$
Donc $Q_1$ est la 6ème note. Il s'agit d'un 9.
Donc $Q_1=9$.
On calcule ${75}/{100}×22=16,5$
Donc $Q_3$ est la 17ème note. Il s'agit d'un 12.
Donc $Q_3=12$.
Et finalement, on obtient: $EI=Q_3-Q_1=12-9=3$.
L'écart interquartile de la seconde série vaut 3.
Après les manifestations de bienveillance du professeur, on trouve (à la calculatrice) que la nouvelle moyenne vaut environ 10,82
et le nouvel écart-type vaut environ 2,21.
Les notes faibles ayant été relevées, la moyenne a augmenté, et, comme la dispersion des notes est plus faible, l'écart-type a baissé.
La médiane reste à 11. De plus, $Q_1$ et $Q_3$ n'ont pas changé, et donc l'écart interquartile non plus.
Ces résultats confirment que le couple ($m$ ; $EI$) n'est pas sensible aux valeurs extrêmes de la série, alors que le couple ($x↖{−}$ ; $σ$) l'est.