 Les vecteurs
Les vecteurs
I. Vecteurs et translations
Définition
Un vecteur non nul du plan est un "objet mathématique" caractérisé par 3 paramètres: sa direction, son sens et sa longueur.
On le représente souvent par une "flèche". L'endroit où l'on dessine la "flèche" n'a aucune importance.
Le vecteur nul a une longueur nulle. Il n'a ni direction, ni sens particulier.
La notation des vecteurs est caractérisée par la flèche qui les surmonte.
Par exemple, le vecteur nul est noté ${0}↖{→}$
Le graphique ci-dessous représente un vecteur ${u}↖{→}$ (flèche verte).
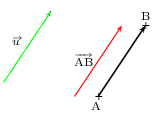
On a placé deux points A et B tels que ${AB}↖{→}={u}↖{→}$
(les flèches vertes, rouge et noire ont même direction, même sens et même longueur). On dit alors que
${AB}↖{→}$ est un représentant du vecteur ${u}↖{→}$.
Exemple
Soient A et B deux points distincts du plan.
Le vecteur ${AB}↖{→}$ a pour direction celle de la droite (AB), son sens est de A vers B, et sa longueur est la distance AB.
Le vecteur ${BA}↖{→}$ a même direction et même longueur que le vecteur ${AB}↖{→}$, mais il est de sens opposé.
Le vecteur ${AA}↖{→}$ est le vecteur nul; on a donc: ${AA}↖{→}={0}↖{→}$.
Définition
La norme du vecteur ${u}↖{→}$ est sa longueur; on la note: $∥{u}↖{→}∥$
Exemple
Soient A et B deux points du plan. On a alors: $∥{AB}↖{→}∥=AB$.
Propriété
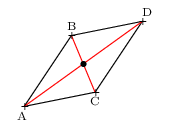
ABDC est un parallélogramme
si et seulement si
[AD] et [BC] ont même milieu.
Propriété
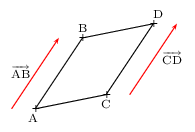
ABDC est un parallélogramme
si et seulement si ${AB}↖{→}={CD}↖{→}$.
Définition
Soient A et B deux points du plan
La translation qui transforme A en B est l'application qui à tout point M du plan associe le point M' tel que le quadrilatère ABM'M soit un parallélogramme.
Une telle translation s'appelle translation de vecteur ${AB}↖{→}$.
On la note souvent: $t_{{AB}↖{→}}$
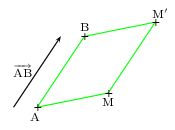
Ici, l'image du point M par la translation de vecteur ${AB}↖{→}$ est le point M'; on note: $t_{{AB}↖{→}}(M)=M'$
Définition et propriétés
Une translation est associée à un vecteur unique.
La translation identité, qui transforme tout point en lui-même, est associée au vecteur nul.
A retenir
La propriété essentielle suivante, qui résume les propriétés précédentes.
Propriété essentielle
ABDC est un parallélogramme $⇔$ ${AB}↖{→}={CD}↖{→}$ $⇔$ $t_{{AB}↖{→}}(C)=D$

Exemple
EFGH est un parallélogramme.
Compléter les propositions qui suivent.
${EF}↖{→}= ...$
${FE}↖{→}= ...$
${FG}↖{→}= ...$
$t_{{EF}↖{→}}(H)=...$
$t_{{FG}↖{→}}(E)=...$
Corrigé
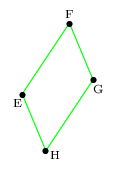
EFGH est un parallélogramme, donc:
${EF}↖{→}= {HG}↖{→}$
${FE}↖{→}= {GH}↖{→}$
${FG}↖{→}= {EH}↖{→}$
$t_{{EF}↖{→}}(H)=G$
$t_{{FG}↖{→}}(E)=H$
II. Somme de vecteurs
Définition et propriété
Soient ${u}↖{→}$ et ${v}↖{→}$ deux vecteurs du plan
L'enchaînement des translations $t_{{u}↖{→}}$ et $t_{{v}↖{→}}$ est une nouvelle translation dont le vecteur est noté ${u}↖{→}+{v}↖{→}$.
Par conséquent:
Si $t_{{u}↖{→}}(M)=M'$ et si $t_{{v}↖{→}}(M')=M"$, alors $t_{{u}↖{→}+{v}↖{→}}(M)=M"$.
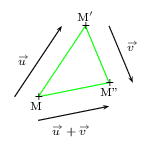
Construction pratique de la somme ${u}↖{→}+{v}↖{→}$
On dessine les vecteurs l'un derrière l'autre
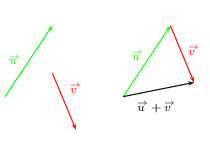
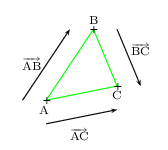
Relation de Chasles
Pour tous points A, B et C, on a:
${AB}↖{→}+{BC}↖{→}={AC}↖{→}$.
Exemple
Calculer ${u}↖{→}={FA}↖{→}+ {BE}↖{→}+ {AB}↖{→}+ {EF}↖{→} $.
Corrigé
On réordonne les vecteurs et on applique plusieurs fois la relation de Chasles.
On obtient: ${u}↖{→}={FA}↖{→}+ {BE}↖{→}+ {AB}↖{→}+ {EF}↖{→}=({FA}↖{→}+{AB}↖{→})+ ({BE}↖{→}+ {EF}↖{→}) $
Donc: ${u}↖{→}={FB}↖{→}+ {BF}↖{→} $ (d'après la relation de Chasles)
Donc: ${u}↖{→}={FF}↖{→} $ (d'après la relation de Chasles)
Donc: ${u}↖{→}={0}↖{→} $
Règle du parallélogramme
Pour tous points O, A, B et M, on a l'équivalence:
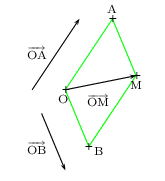
OAMB est un parallélogramme $⇔$ ${OA}↖{→}+{OB}↖{→}={OM}↖{→}$.
Exemple
X, Y, Z et T sont 4 points tels que ${XY}↖{→}+{XT}↖{→}={XZ}↖{→}$.
Montrer que ${XY}↖{→}={TZ}↖{→}$
Corrigé
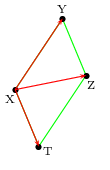
${XY}↖{→}+{XT}↖{→}={XZ}↖{→}$
Donc XYZT est un parallélogramme.
Donc: ${XY}↖{→}={TZ}↖{→}$
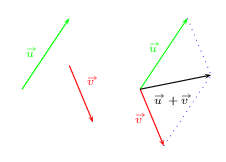
Seconde méthode pour construire la somme ${u}↖{→}+{v}↖{→}$
On dessine les vecteurs issus d'un même point et un parallélogramme
Attention !
Ne pas confondre la relation de Chasles (qui utilise 3 points) et la règle du parallélogramme (qui utilise 4 points).
III. Différence de vecteurs
Définition
L'opposé d'un vecteur ${u}↖{→}$ est noté $-{u}↖{→}$.
L'opposé d'un vecteur non nul ${u}↖{→}$ est le vecteur de même direction et de même longueur que le vecteur ${u}↖{→}$,
mais de sens opposé.
Par ailleurs, on a: $-{0}↖{→}={0}↖{→}$
Propriété
Soient A et B deux points.
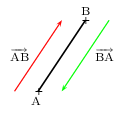
L'opposé du vecteur ${AB}↖{→}$ est le vecteur ${BA}↖{→}$
On a donc: $-{AB}↖{→}={BA}↖{→}$.
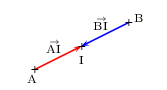
Propriété
I est le milieu de [AB] $⇔$ ${AI}↖{→}=-{BI}↖{→}$ $⇔$ ${AI}↖{→}={IB}↖{→}$
Définition
Soient ${u}↖{→}$ et ${v}↖{→}$ deux vecteurs du plan
La différence ${u}↖{→}-{v}↖{→}$ est définie par l'égalité: ${u}↖{→}-{v}↖{→}={u}↖{→}+(-{v}↖{→})$
Exemple
On sait que: ${YZ}↖{→}-{TZ}↖{→}+{XY}↖{→}=-{VT}↖{→}$.
Que dire de T?
Corrigé
On va éliminer les signes - et utiliser la relation de Chasles.
On a: ${YZ}↖{→}-{TZ}↖{→}+{XY}↖{→}=-{VT}↖{→}$.
Donc: ${YZ}↖{→}+{ZT}↖{→}+{XY}↖{→}=+{TV}↖{→}$.
Donc: ${XY}↖{→}+{YZ}↖{→}+{ZT}↖{→}={TV}↖{→}$ (on a réordonné)
Donc: ${XT}↖{→}={TV}↖{→}$ (d'après la relation de Chasles).
Donc T est le milieu du segment [XV].
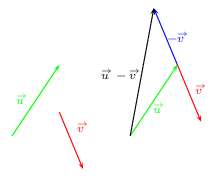
Construction pratique de la différence ${u}↖{→}-{v}↖{→}$
Il suffit d'utiliser la définition ${u}↖{→}-{v}↖{→}={u}↖{→}+(-{v}↖{→})$,
et, par exemple, de dessiner les vecteurs ${u}↖{→}$ et $-{v}↖{→}$ l'un derrière l'autre.
IV. Produit d'un vecteur par un nombre réel
Définition
Soit ${u}↖{→}$ un vecteur et $k$ un nombre réel
Si $k=0$ ou si ${u}↖{→}={0}↖{→}$, alors $k.{u}↖{→}={0}↖{→}$
Sinon:
si $k>0$, alors $k.{u}↖{→}$ est un vecteur de même direction et de même sens que ${u}↖{→}$, et dont la longueur vaut $k×∥{u}↖{→}∥$.
si $k<0$, alors $k.{u}↖{→}$ est un vecteur de même direction que ${u}↖{→}$, de sens opposé à celui de ${u}↖{→}$, et dont la longueur vaut $-k×∥{u}↖{→}∥$.
Exemple
Placer les points C et D définis par ${AC}↖{→}=2,5.{AB}↖{→}$ et ${AD}↖{→}=-0,5.{AB}↖{→}$
Corrigé
Voici les points C et D correctement placés.

Propriété
Pour tous vecteurs ${u}↖{→}$ et ${v}↖{→}$ et tous réels $k$ et $k'$, on a:
$k.({u}↖{→}+{v}↖{→})=k.{u}↖{→}+k.{v}↖{→}$
$(k+k').{u}↖{→}=k.{u}↖{→}+k'.{u}↖{→}$
$k.{u}↖{→}={0}↖{→}$ $⇔$ $k=0$ ou ${u}↖{→}={0}↖{→}$
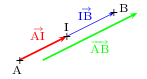
Propriété
I est le milieu de [AB] $⇔$ ${AB}↖{→}=2.{AI}↖{→}$ $⇔$ ${AB}↖{→}=2.{IB}↖{→}$
Définition
Deux vecteurs non nuls ${u}↖{→}$ et ${v}↖{→}$ sont colinéaires si et seulement si
il existe un réel $k$ tel que ${v}↖{→}=k.{u}↖{→}$
Le vecteur nul ${0}↖{→}$ est colinéaire à tout vecteur.
Propriété
Les points A, B et C sont alignés $⇔$ les vecteurs ${AB}↖{→}$ et ${AC}↖{→}$ sont colinéaires

Exemple
Placer les points E et D définis par:
${AD}↖{→}={AB}↖{→}+{AC}↖{→}$ et ${AE}↖{→}=2,5.{AB}↖{→}+2,5.{AC}↖{→}$
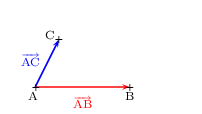
Montrer que A, D et E sont alignés.
Corrigé
Voici les points D et E correctement placés.
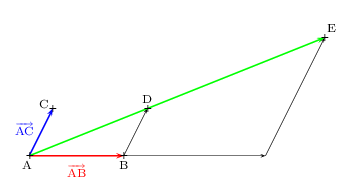
On a: ${AE}↖{→}=2,5.{AB}↖{→}+2,5.{AC}↖{→}$
Donc: ${AE}↖{→}=2,5.({AB}↖{→}+{AC}↖{→})$
Donc: ${AE}↖{→}=2,5.{AD}↖{→}$
Donc les vecteurs ${AE}↖{→}$ et ${AD}↖{→}$ sont colinéaires.
Donc les points A, D et E sont alignés.
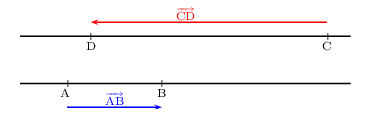
Propriété
Soient A, B, C et D quatre points distincts deux à deux.
Les droites (AB) et (CD) sont parallèles $⇔$ les vecteurs ${AB}↖{→}$ et ${CD}↖{→}$ sont colinéaires
V. Coordonnées et vecteurs
Définition et propriété
Le plan est muni d'un repère $(O,I,J)$ quelconque.
Pour tout vecteur ${u}↖{→}$, il existe un unique couple $(x;y)$ de nombres réels tel que ${u}↖{→}=x.{OI}↖{→}+y.{OJ}↖{→}$
$(x;y)$ s'appelle couple des coordonnées de ${u}↖{→}$.
Remarque: on note indifféremment ${u}↖{→}(x,y)$ ou ${u}↖{→}(\table x; y)$.
La première coordonnée, $x$, est l'abscisse; la seconde coordonnée, $y$, est l'ordonnée.
Propriété
Le point M a pour coordonnées $(x;y)$ dans le repère $(O,I,J)$
si et seulement si
le vecteur ${OM}↖{→}$ a pour coordonnées $(x;y)$ dans le repère $(O,I,J)$
Exemple
Soient A, B et C trois points non alignés. On suppose que: ${AD}↖{→}=2.{AB}↖{→}+{AC}↖{→}$
- Faire une figure
- Quelles sont les coordonnées de D dans le repère $(A,B,C)$?
- Une question plus difficile!
Quelles sont les coordonnées de D dans le repère $(C,B,A)$?
Corrigé
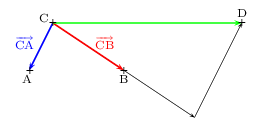
- Voici une figure convenable
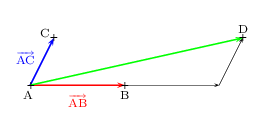
- Comme ${AD}↖{→}=2.{AB}↖{→}+1.{AC}↖{→}$, le point D a pour coordonnées $(2;1)$ dans le repère $(A,B,C)$.
- On cherche les coordonnées de D dans le repère $(C,B,A)$. Il suffit donc d'exprimer ${CD}↖{→}$ en fonction de ${CB}↖{→}$ et ${CA}↖{→}$.
Nous allons faire apparaître ces vecteurs à l'aide de la relation de Chasles à partir de l'hypothèse.
On a: ${AD}↖{→}=2.{AB}↖{→}+{AC}↖{→}$
Et donc: ${AC}↖{→}+{CD}↖{→}=2.({AC}↖{→}+{CB}↖{→})+{AC}↖{→}$ (d'après la relation de Chasles)
Donc: ${AC}↖{→}+{CD}↖{→}=2.{AC}↖{→}+2.{CB}↖{→}+{AC}↖{→}$
Donc: ${CD}↖{→}=2.{AC}↖{→}+2.{CB}↖{→}+{AC}↖{→}-{AC}↖{→}$
Donc: ${CD}↖{→}=2.{AC}↖{→}+2.{CB}↖{→}$
Donc: ${CD}↖{→}=-2.{CA}↖{→}+2.{CB}↖{→}$
Soit: ${CD}↖{→}=2.{CB}↖{→}-2.{CA}↖{→}$
Et par là, le point D a pour coordonnées $(2;-2)$ dans le repère $(C,B,A)$.
Cela se lit sur la figure qui suit.
Propriété
Le plan est muni d'un repère.
Soient ${u}↖{→}(\,x\,;\,y\,)$ et ${v}↖{→}(\,x'\,;\,y'\,)$ deux vecteurs et $k$ un réel.
${u}↖{→}+{v}↖{→}$ a pour coordonnées $(\,x+x'\,;\,y+y'\,)$
$k.{u}↖{→}$ a pour coordonnées $(\,kx\,;\,ky\,)$
Propriété
Le plan est muni d'un repère orthonormé.
Soit ${u}↖{→}(\,x\,;\,y\,)$ un vecteur
$∥{u}↖{→}∥=√ {x^2+y^2}$
Exemple
Le plan est muni d'un repère orthonormé.
Soient ${u}↖{→}(\,2\,;\,-5\,)$ et ${v}↖{→}(\,6\,;\,-7\,)$ deux vecteurs.
Quelles sont les coordonnées de ${w}↖{→}=3.{u}↖{→}+{v}↖{→}$?
Déterminer la norme de ${w}↖{→}$.
Corrigé
On obtient: $3.{u}↖{→}+{v}↖{→}(\,3×2+6\,;\,3×(-5)+(-7)\,)$
Soit: $3.{u}↖{→}+{v}↖{→}(\,12\,;\,-22\,)$
Et comme le repère est orthonormé, la norme de ${w}↖{→}$ est:
$∥{w}↖{→}∥=√ {12^2+(-22)^2}=√ {628}≈25,06$
Propriété
Le plan est muni d'un repère.
Soient $A(\,x_A\,;\,y_A\,)$ et $B(\,x_B\,;\,y_B\,)$ deux points.
Le vecteur ${AB}↖{→}$ a pour coordonnées $(\,x_B-x_A\,;\,y_B-y_A\,)$
Exemple
Le plan est muni d'un repère.
Soient $A(\,2\,;\,1,5\,)$ et $B(\,5\,;\,-1\,)$ deux pointss.
Faire une figure.
Lire graphiquement les coordonnées de ${AB}↖{→}$, puis les retrouver par un calcul.
Corrigé
Voici une figure convenable.
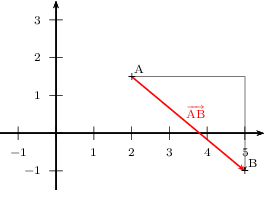
Graphiquement, on constate que ${AB}↖{→}(\,3\,;\,-2,5\,)$
En effet, pour aller de A en B, on a avancé de 3, puis on a descendu de 2,5.
Retrouvons ces valeurs par le calcul.
On a: $x_{{AB}↖{→}}=x_B-x_A=5-2=3$
et: $y_{{AB}↖{→}}=y_B-y_A=-1-1,5=-2,5$
On a donc bien: ${AB}↖{→}(\,3\,;\,-2,5\,)$
Définition
Le plan est muni d'un repère $(O,I,J)$ quelconque.
Soient ${u}↖{→}(x,y)$ et ${v}↖{→}(x',y')$ deux vecteurs.
Le déterminant du couple $({u}↖{→},{v}↖{→})$, noté $det({u}↖{→},{v}↖{→})$, est le nombre réel défini par
$det({u}↖{→},{v}↖{→})=xy'-x'y$
Propriété
Le plan est muni d'un repère.
Soient ${u}↖{→}$ et ${v}↖{→}$ deux vecteurs.
${u}↖{→}$ et ${v}↖{→}$ sont colinéaires $⇔$ $det({u}↖{→},{v}↖{→})=0$
Exemple
Le plan est muni d'un repère.
Soient $A(\,2\,;\,1,5\,)$, $B(\,5\,;\,-1\,)$ et $C(\,-2\,;\,y\,)$ trois points.
Déterminer $y$ tel que A, B et C soient alignés.
Corrigé
A, B et C sont alignés $⇔$ ${AB}↖{→}$ et ${AC}↖{→}$ sont colinéaires
$⇔$ $det({AB}↖{→},{AC}↖{→})=0$
Or, on obtient facilement: ${AB}↖{→}(\,3\,;\,-2,5\,)$ et ${AC}↖{→}(\,-4\,;\,y-1,5\,)$
Et donc: $det({AB}↖{→},{AC}↖{→})=3×(y-1,5)-(-4)×(-2,5)=3y-4,5-10=3y-14,5$
Par conséquent:
A, B et C sont alignés $⇔$ $3y-14,5=0$
$⇔$ $y={14,5}/{3}≈4,83$
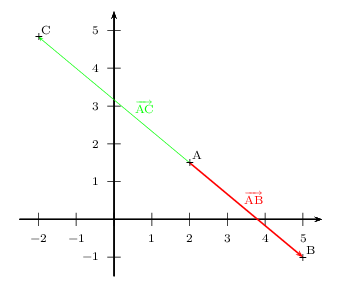
Le résultat obtenu semble confirmé par le graphique.
Propriété
Le plan est muni d'un repère orthonormé.
Si ABCD est un parallélogramme, alors son aire est égale à $|det({AB}↖{→},{AD}↖{→})|$
Exemple
Le plan est muni d'un repère orthonormé $(O,I,J)$.
Soient $O(\,0\,;\,0\,)$, $E(\,3\,;\,1\,)$, $F(\,4\,;\,2\,)$ et $G(\,x_G\,;\,y_G\,)$ quatre points tels que OEFG soit un parallélogramme.
Déterminer l'aire $s$ de OEFG.
Corrigé
OEFG est un parallélogramme
Donc $s=|det({EF}↖{→},{EO}↖{→})|$
Or, on obtient facilement: ${EF}↖{→}(\,1\,;\,1\,)$ et ${EO}↖{→}(\,-3\,;\,-1\,)$
Et donc: $det({EF}↖{→},{EO}↖{→})=1×(-1)-(-3)×1=-1+3=2$
Et comme le repère est orthonormé, on obtient:
$s=|det({EF}↖{→},{EO}↖{→})|$
Soit: $s=2$ (unités d'aire)
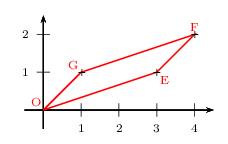
Autre méthode.
Comme OEFG est un parallélogramme, on a aussi: $s=|det({OG}↖{→},{OF}↖{→})|$
Cherchons les coordonnées de G.
OEFG est un parallélogramme $⇔$ ${OG}↖{→}={EF}↖{→}$
$⇔$ $x_G=1$ et $y_G=1$
Donc $G(\,1\,;\,1\,)$, et par là, on obtient: ${OG}↖{→}(\,1\,;\,1\,)$
Et comme ${OF}↖{→}(\,4\,;\,2\,)$, on a: $det({OG}↖{→},{OF}↖{→})=1×2-4×1=-2$
Et donc on retrouve: $s=|-2|=2$