Les fonctions affines
Les fonctions affines
Exercice 1
Toutes les réponses aux questions qui suivent se trouvent graphiquement. Néanmoins, il est demandé de justifier rapidement vos réponses.
Voici les représentations graphiques des fonctions $f$, $v$, $b$, $r$, $n$ et $g$, définies sur l'intervalle [0;5].
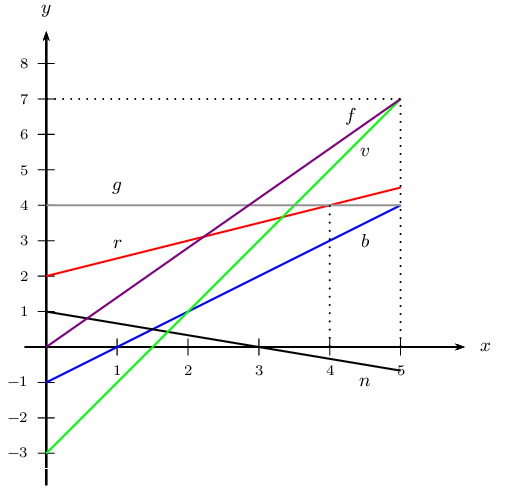
1. Déterminer les expressions donnant $f(x)$, $v(x)$, $b(x)$, $r(x)$, $n(x)$ et $g(x)$ pour tout $x$ de l'intervalle [0;5].
2. Déterminer algébriquement les coordonnées du point d'intersection du segment représentant $n$ et de celui représentant $v$.
3. Résoudre algébriquement l'inéquation $b(x)≤n(x)$ sur l'intervalle [0;5].
Corrigé

1. Chaque représentation proposée est un segment de droite. Par conséquent, les 5 fonctions cherchées sont affines.
Pour chacune d'elles, l'expression cherchée est donc du type $ax+b$, où $a$ est le coefficient directeur du segment de droite,
et où $b$ est l'ordonnée à l'origine de la droite associée.
Première fonction
Commençons par $f(x)$.
La fonction $f$ est une fonction affine particulière, car la droite qui lui est associée passe par l'origine. C'est une fonction linéaire.
On a donc: $b=0$.
Cherchons la valeur du coefficient directeur $a$.
Méthode 1: On se place sur la droite, de préférence en un point dont les coordonnées sont faciles à déterminer.
Puis il suffit de se déplacer de 1 unité parallèlement à l'axe des abscisses vers la droite.
Puis on regagne la droite en se déplaçant parallèlement à l'axe des ordonnées.
La valeur du déplacement, comptée positivement vers le haut, et négativement vers le bas, est égale à $a$.
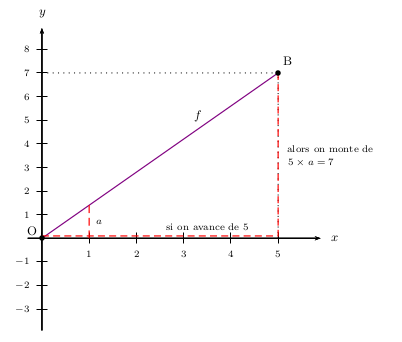
Partons donc du point O. La méthode précédente est imprécise, car le déplacement de $a$ vers le haut est difficile à évaluer.
Nous choisissons un déplacement de 5 unités "horizontales", ce qui occasionne un déplacement de 7 unités "verticales".
Le déplacement "vertical" étant proportionnel au déplacement "horizontal", ce déplacement vertical vaut donc $5×a$.
Nous obtenons donc l'égalité: $5a=7$, ce qui donne: $a={7}/{5}=1,4$.
Finalement, l'expression cherchée est: $f(x)=1,4x$.
Méthode 2: On repère sur la droite 2 points A et B dont les coordonnées sont faciles à déterminer.
Puis il suffit d'appliquer la formule $a={y_B-y_A}/{x_B-x_A}$.
Les points $O(0;0)$ et $B(5;7)$ sont sur la droite.
Donc $a={y_B-y_O}/{x_B-x_O}={7-0}/{5-0}={7}/{5}=1,4$.
Finalement, l'expression cherchée est: $f(x)=1,4x$.
Seconde fonction
Déterminons maintenant $v(x)$.
On a vu que $v(x)=ax+b$.
$b$, ordonnée à l'origine, vaut $-3$.
Cherchons la valeur du coefficient directeur $a$.
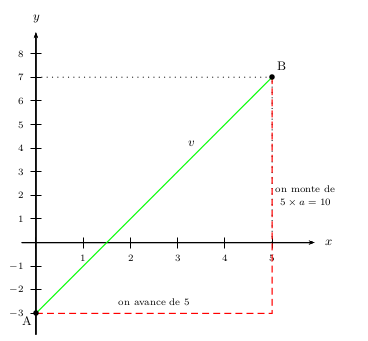
Méthode 1: Nous obtenons facilement: $5a=10$, ce qui donne: $a={10}/{5}=2$.
Méthode 2:Les points $A(0;-3)$ et $B(5;7)$ sont sur la droite.
Donc $a={y_B-y_A}/{x_B-x_A}={7-(-3)}/{5-0}={10}/{5}=2$.
Finalement, l'expression cherchée est: $v(x)=2x-3$.
Dernières fonctions
Déterminons de même $b(x)$, $r(x)$, $n(x)$ et $g(x)$.
Nous obtenons sans difficulté:
$b(x)=1x-1$, soit: $b(x)=x-1$.
$r(x)=0,5x+2$.
$n(x)=-{1}/{3}x+1$. Attention! La fonction est décroissante, et donc $a$ est négatif.
$g(x)=0x+4$. Soit: $g(x)=4$. Attention! La fonction est constante, et donc $a$ est nul.
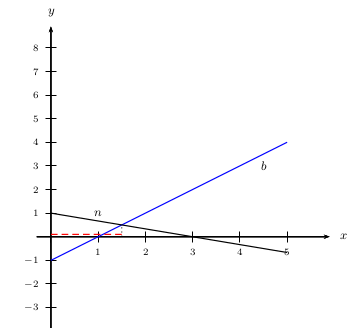
2. Soit $M(x;y)$ le point d'intersection cherché.
Comme il est sur $n$, on a: $y=n(x)$.
Comme il est sur $v$, on a: $y=v(x)$.
Par conséquent, il suffit de résoudre l'équation $n(x)=v(x)$ pour déterminer $x$.
Résolution: $n(x)=v(x)$ $⇔$ $-{1}/{3}x+1=2x-3$ $⇔$ $-{1}/{3}x+1-2x+3=0$
A retenir: dans une équation, il est conseillé de commencer par rendre le membre de droite égal à 0.
On continue: $n(x)=v(x)$ $⇔$ $(-{1}/{3}-{6}/{3})x+1+3=0$ $⇔$ ${-7}/{3}x+4=0$
A retenir: dans une équation, si le membre de gauche est affine, alors il est facile d'isoler $x$.
On continue: $n(x)=v(x)$ $⇔$ ${-7}/{3}x=-4$ $⇔$ $x=-4×{3}/{-7}$
A retenir: diviser par un nombre, c'est multiplier par son inverse.
On termine: $n(x)=v(x)$ $⇔$ $x={12}/{7}$
Et en reportant dans une des 2 expressions (par exemple $n(x)$), on obtient: $y=2×{12}/{7}-3={24}/{7}-{21}/{7}={3}/{7}$
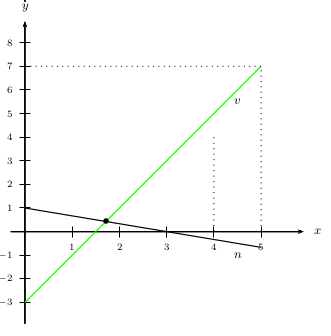
Finalement, le point d'intersection a pour coordonnées $({12}/{7}; {3}/{7})$.
Ces coordonnées semblent conformes au dessin ci-dessous.
3. $b(x)≤n(x)$ $⇔$ $x-1≤-{1}/{3}x+1$ $⇔$ $x-1+{1}/{3}x-1≤0$
A retenir: dans une inéquation, il est conseillé de commencer par rendre le membre de droite égal à 0.
On continue: $b(x)≤n(x)$ $⇔$ $(1+{1}/{3})x-1-1≤0$ $⇔$ $({3}/{3}+{1}/{3})x-2≤0$ $⇔$ ${4}/{3}x-2≤0$
A retenir: dans une inéquation, si le membre de gauche est affine, alors il est facile d'isoler $x$.
On continue: $b(x)≤n(x)$ $⇔$ ${4}/{3}x≤2$ $⇔$ $x≤2×{3}/{4}$
A retenir: dans une inéquation, si l'on divise les 2 membres par un nombre strictement positif, alors le sens de l'inégalité ne change pas.
On termine: $b(x)≤n(x)$ $⇔$ $x≤1,5$
Comme on résout sur l'intervalle $[0;5]$, l'ensemble des solutions sont les nombres compris entre 0 et $1,5$.
On note: $\S=[0;1,5]$.
Les solutions se voient clairement sur le dessin ci-dessous.