 Les fonctions affines
Les fonctions affines
Exercice 2
La droite $d_1$ est la représentation graphique de la fonction $f$.
La droite $d_2$ est la représentation graphique de la fonction $g$.
La droite $d_3$ est la représentation graphique de la fonction $h$.
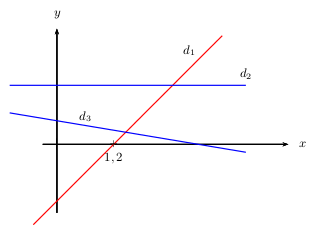
Attention! L'échelle de l'axe des ordonnées est inconnue.
1. Expliquer pourquoi ces 3 fonctions admettent chacune une expression du type $mx+p$.
2.a. On admet que, pour la fonction $f$, on a: soit $p=2$, soit $p=0$, soit $p=-2,4$.
Quelle est la valeur de $p$? Expliquer votre choix.
2.b. On admet que, pour la fonction $f$, on a: soit $m=2,1$, soit $m=2$, soit $m=-2,7$.
Quelles est la valeur possible de $m$? Expliquer votre choix.
3. On admet que $d_1$ et $d_2$ se coupent au point d'abscisse $2,45$.
Déterminer l'expression de $g(x)$.
4. On admet que, pour tout réel $x$, on a: soit $h(x)=-x+1$, soit: $h(x)=-{1}/{3}x+1$.
Déterminer l'expression de $h(x)$.
Solution...
Corrigé
1. Les 3 fonctions proposées sont représentées par des droites. Ce sont donc des fonctions affines.
Elles admettent donc chacune une expression du type $mx+p$.

2.a. $p$ est l'ordonnée à l'origine. Or, pour la droite $d_1$, il est clair que $p$ est strictement négatif.
Donc la seule valeur convenable est $p=-2,4$.
2.b. D'après ce qui précède, nous savons donc que $f(x)=mx-2,4$.
Comme $f$ est strictement croissante, on en déduit que le coefficient directeur $m$ est strictement positif.
Donc, par élimination: ou bien $m=2,1$, ou bien $m=2$.
Pour choisir, utilisons le fait que $f(1,2)=0$.
Supposons que $m=2,1$. On a alors: $f(x)=2,1x-2,4$. Et par là: $f(1,2)=2,1×1,2-2,4=0,12$. Comme on ne trouve pas 0, la valeur de $m$ envisagée est exclue.
Donc, par élimination, il ne reste plus que $m=2$.
Pour se rassurer, nous pouvons vérifier que, si $m=2$, alors $f(1,2)=0$.
Dans ce cas, on a alors: $f(x)=2x-2,4$. Et par là: $f(1,2)=2×1,2-2,4=0$. C'est parfait!
3. On pose $g(x)=mx+p$.
Comme $d_2$ est parallèle à l'axe des abscisses, on a: $m=0$.
Et par là, on obtient: $g(x)=p$.
Or, comme $d_1$ et $d_2$ se coupent au point d'abscisse $2,45$, on a donc: $g(2,45)=f(2,45)$.
Soit: $p=2×1,2-2,4$. Soit: $p=2,5$.
Finalement, pour tout nombre réel $x$, on a: $g(x)=2,5$.
4. Si $h(x)=-x+1$, alors: $h(x)=0$ $⇔$ $-x+1=0$ $⇔$ $-x=-1$ $⇔$ $x=1$.
Or, graphiquement, il est clair que, si $h(x)=0$, alors $x$>1,2.
On aurait alors $x=1$ et $x$>1,2, ce qui est absurde.
Donc la formule $h(x)=-x+1$ ne convient pas.
Par élimination, il ne reste plus que $h(x)=-{1}/{3}x+1$.
