Corrigé

1. $f(x)=0$ $⇔$ $2x+1=0$ $⇔$ $2x=-1$ $⇔$ $x={-1}/{2}=-0,5$.
Donc $\S=\{-0,5\}$.

2. $f(x)=g(x)$ $⇔$ $2x+1=0,5x-1$ $⇔$ $2x+1-0,5x+1=0$ $⇔$ $1,5x+2=0$ $⇔$ $x={-2}/{1,5}=-{4}/{3}$.
Donc $\S=\{-{4}/{3}\}$.
A retenir: dans une équation, il est conseillé de commencer par rendre le membre de droite égal à 0. Puis, si le membre de gauche est affine, alors il sera alors facile d'isoler $x$.
Evidemment, les "experts" peuvent "sauter" des étapes, et isoler directement $x$, mais attention aux fautes de calcul!

3. $f(x)×g(x)=0$ $⇔$ $f(x)=0$ ou $g(x)=0$
A retenir: Un produit de facteurs est nul si et seulement si l'un des facteurs est nul.
On obtient donc: $f(x)×g(x)=0$ $⇔$ $2x+1=0$ ou $0,5x-1=0$ $⇔$ $x={-1}/{2}=-0,5$ ou $x={1}/{0,5}=2$.
Donc $\S=\{-0,5;2\}$

4. L'équation ${f(x)}/{g(x)}=0$ est particulière car le domaine de définition de la fonction ${f(x)}/{g(x)}$ n'est pas $ℝ$.
En effet, le dénominateur d'un quotient ne peut être nul, et ici, $g(x)$ s'annule pour $x=2$.
La valeur 2 est dite "valeur interdite".
Le domaine de définition de la fonction ${f(x)}/{g(x)}$ est donc $ℝ\ ∖\{2\}$.
Ce sera le domaine dans lequel on cherchera les solutions de l'équation.
On a donc: $\D_E=ℝ\ ∖\{2\}$.
Résolution: ${f(x)}/{g(x)}=0$ $⇔$ $f(x)=0$.
A retenir: Un quotient est nul si et seulement si son numérateur est nul.
On obtient donc: ${f(x)}/{g(x)}=0$ $⇔$ $2x+1=0$ $⇔$ $x={-1}/{2}=-0,5$.
Donc $\S=\{-0,5\}$.
Attention! Nous n'avons pas oublié de vérifier que la solution trouvée fait bien partie de $\D_E$.

5. A retenir: pour dresser le tableau de signes d'une fonction affine (non constante), il suffit de repérer pour quelle valeur elle s'annule. A droite de cette valeur, elle sera du signe de son coefficient directeur.
$f$ est affine.
Or: $f(x)=0$ $⇔$ $x=-0,5$.
Et de plus, le coefficient directeur de $f$ est strictement positif (il vaut 2).
D'où le tableau de signe suivant:


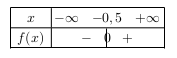
6. $g$ est affine.
Or: $g(x)=0$ $⇔$ $0,5x-1=0$ $⇔$ $x={1}/{0,5}=2$.
Et de plus, le coefficient directeur de $g$ est strictement positif (il vaut 0,5).
D'où le tableau de signes suivant:


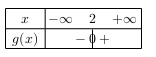
7. $h$ est affine.
Or: $h(x)=0$ $⇔$ $-x+2=0$ $⇔$ $x={-2}/{-1}=2$.
Et de plus, le coefficient directeur de $h$ est strictement négatif (il vaut $-1$).
D'où le tableau de signes suivant:


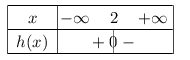
8. Considérons l'inéquation: $f(x)×g(x)≤0$.
A retenir: dans une inéquation, il est conseillé de commencer par rendre le membre de droite égal à 0.
Ici, c'est déjà le cas. Donc la première étape est terminée.
Puis, si le membre de gauche est une fonction affine, il est alors facile d'isoler $x$.
Ici, le membre de gauche n'est pas affine. Donc nous devons procéder autrement!
Il est alors conseillé de présenter ce membre de gauche sous forme d'un produit (ou d'un quotient).
Ici, c'est déjà le cas. Donc la seconde étape est terminée.
Il reste alors à étudier le signe de ce membre de gauche pour pouvoir conclure!
Nous allons tout d'abord dresser le tableau de signes du produit $p(x)=f(x)×g(x)$.
Nous utilisons les tableaux de signes précédents pour construire le tableau suivant:

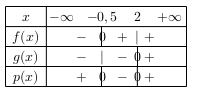
Comme nous cherchons pour quelles valeurs de $x$ le produit $p(x)$ est inférieur ou égal à 0, nous en déduisons que l'ensemble des solutions est:
$\S=[-0,5;2 ]$.

9. Considérons l'inéquation: $f(x)×g(x)>0$.
L'essentiel a déjà été fait dans la question précédente!
Nous cherchons cette fois-ci pour quelles valeurs de $x$ le produit $p(x)$ est strictement supérieur à 0. D'après le tableau de signes du produit $p(x)$, nous en déduisons que l'ensemble des solutions est:
$\S=]- ∞;-0,5[∪]2;+ ∞[$.

10. Considérons l'inéquation: ${f(x)}/{g(x)}≤0$.
La méthode est encore la même que précédemment, excepté que, cette fois-ci, nous allons chercher le signe du quotient $q(x)={f(x)}/{g(x)}$.
Evidemment, nous avons remarqué que le quotient n'existe pas si $g(x)=0$, c'est à dire si $x=2$. Cette valeur "interdite" entraîne l'apparition d'une "double-barre" dans le tableau, pour bien montrer que le réel 2 n'a pas d'image par $q$.
Nous obtenons alors le tableau de signes ci-dessous.

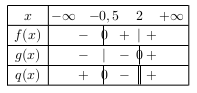
Comme nous cherchons pour quelles valeurs de $x$ le quotientt $q(x)$ est inférieur ou égal à 0, nous en déduisons que l'ensemble des solutions est:
$\S=[-0,5;2 [$.
Remarque: les solutions sont presque les mêmes qu'au 8., excepté la valeur interdite 2.