Les fonctions affines
Les fonctions affines
Exercice 6
On considère les fonctions $f$ et $h$ représentées ci-dessous.
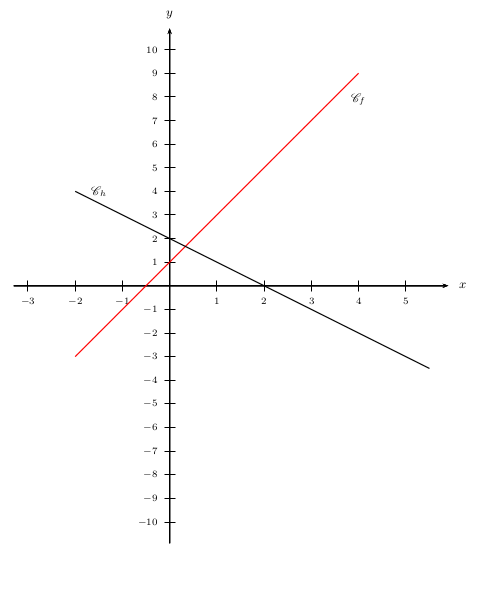
1. Quelle est la nature des fonctions tracées?
2. Résoudre graphiquement l'équation: $f(x)×h(x)=0$.
3. Résoudre graphiquement l'équation: ${f(x)}/{h(x)}=0$.
4. Résoudre graphiquement l'inéquation: $f(x)×h(x)≤0$.
5. Résoudre graphiquement l'inéquation: ${f(x)}/{h(x)}≤0$.
Solution...
Corrigé
1. Les fonctions tracées sont représentées par des droites. Ce sont donc des fonctions affines.
2. $f(x)×h(x)=0$ $⇔$ $f(x)=0$ ou $h(x)=0$
$⇔$ $x=-0,5$ ou $x=2$.
Donc $\S=\{-0,5;2\}$
3. On considère l'équation: ${f(x)}/{h(x)}=0$.
Le membre de gauche est un quotient. On doit avoir: $h(x)≠0$, c'est à dire: $x≠2$.
Résolution: ${f(x)}/{h(x)}=0$ $⇔$ $f(x)=0$ $⇔$ $x=-0,5$.
Donc $\S=\{-0,5\}$.
Remarque: la solution trouvée n'est pas la valeur interdite, sinon, elle aurait été rejetée.
4. Considérons l'inéquation: $f(x)×h(x)≤0$.
Nous allons tout d'abord dresser le tableau de signes du produit $p(x)=f(x)×h(x)$.
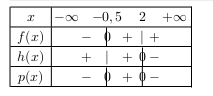
Comme nous cherchons pour quelles valeurs de $x$ le produit $p(x)$ est inférieur ou égal à 0, nous en déduisons que l'ensemble des solutions est:
$\S=]- ∞;-0,5]∪[2;+ ∞[$.
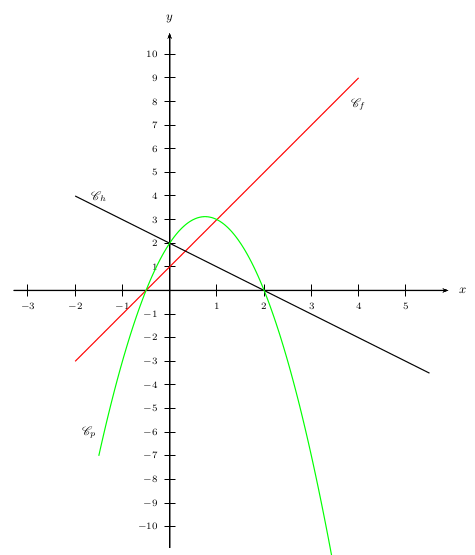
Pour les curieux, j'ai tracé ci-dessous la fonction produit $p$, qui est un produit de 2 fonctions affines.
Les solutions trouvées se vérifient graphiquement.
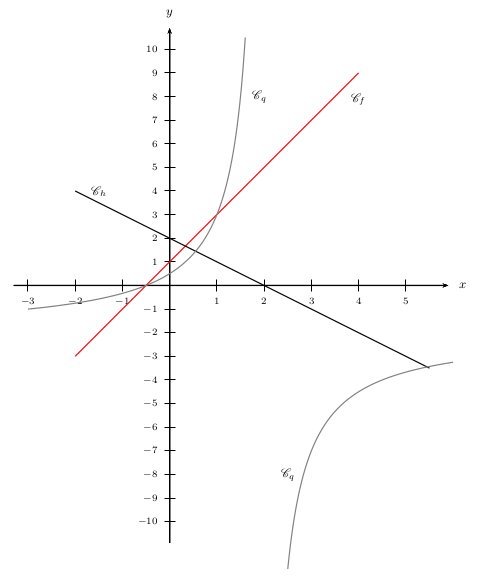
5. Considérons l'inéquation: ${f(x)}/{h(x)}≤0$.
La méthode est encore la même que précédemment, excepté que, cette fois-ci, nous allons chercher le signe du quotient $q(x)={f(x)}/{h(x)}$.
Evidemment, nous avons remarqué que le quotient n'existe pas si $h(x)=0$, c'est à dire si $x=2$. Cette valeur "interdite" entraîne l'apparition d'une "double-barre"
dans le tableau, pour bien montrer que le réel 2 n'a pas d'image par $q$.
Nous obtenons alors le tableau de signes ci-dessous.
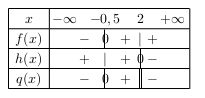
Comme nous cherchons pour quelles valeurs de $x$ le quotientt $q(x)$ est inférieur ou égal à 0, nous en déduisons que l'ensemble des solutions est:
$\S=]- ∞;-0,5]∪]2;+ ∞[$.
Remarque: les solutions sont presque les mêmes qu'au 4., excepté la valeur interdite 2.
Pour les curieux, j'ai tracé ci-dessous la fonction quotient $q$, qui est un quotient de 2 fonctions affines.
Les solutions trouvées se vérifient graphiquement.