 Les fonctions affines
Les fonctions affines
Exercice 7
Partie A
Résoudre l'équation (E1): ${1}/{3}x+1=2-x$, puis interpréter graphiquement.
Résoudre l'équation (E2): $(x+1)(-x+7)=0$.
Résoudre l'équation (E3): ${-x+2}/{3x-1}=0$
Résoudre l'équation (E4): $x^2=x$
Résoudre l'équation (E5): $x^2+6x=-9$
Partie B
Résoudre l'inéquation (In1): $2x+1≤0$.
Résoudre l'inéquation (In2): $-3x+7<0$.
Rappel: dans un système, l'accolade signifie que les lignes sont reliées implicitement par des "et".
Par exemple, dans le système (S1), on cherche les "x" qui vérifient à la fois $x-2>2$ et $-5x<6$.
Résoudre le système d'inéquations (S1): $\{\table x-1>2; -5x<6$
Résoudre le système d'inéquations (S2): $\{\table 2x-3>4; 5x<35$
Résoudre le système d'inéquations (S3): $\{\table 2x+3<x; -2x<6$
Solution...
Corrigé
Partie A
Equation (E1)
On annule le membre de droite.
(E1) $⇔$ ${1}/{3}x+1-2+x=0$
(E1) $⇔$ $({1}/{3}+1)x-1=0$
(E1) $⇔$ $({1}/{3}+{3}/{3})x-1=0$
(E1) $⇔$ ${4}/{3}x-1=0$
On constate que (E1) est une équation du premier degré.
Il est facile d'isoler le $x$.
(E1) $⇔$ ${4}/{3}x=1$ (On a additionné $1$ à chaque membre)
(E) $⇔$ $x=1×{3}/{4}$ (On a multiplié chaque membre par ${3}/{4}$)
(E) $⇔$ $x={3}/{4}=0,75$
Donc $\S=\{\,0,75\,\}$
Interprétation graphique
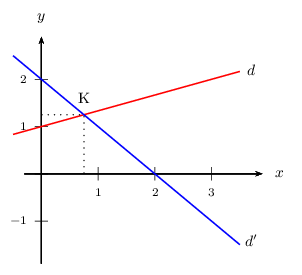
On trace la droite $d$ d'équation $y={1}/{3}x+1$. Elle passe par $(0;1)$ et a pour coefficient directeur ${1}/{3}$.
On trace la droite $d'$ d'équation $y=-x+2$. Elle passe par $(0;2)$ et a pour coefficient directeur $-1$.
Les droites $d$ et $d'$ se coupent au point K, dont l'abscisse $0,75$ est solution de l'équation (E1)
Equation (E2)
(E2) $⇔$ $(x+1)(-x+7)=0$ ((E2) n'est pas une équation du premier degré; le membre de droite est nul, et le membre de gauche est déjà factorisé).
(E2) $⇔$ $x+1=0$ ou $-x+7=0$ (on s'est ramené à deux équations du premier degré).
(E2) $⇔$ $x=-1$ ou $x=7$
Donc $\S=\{\,-1\,;\,7\,\}$
Equation (E3)
Un quotient n'existe que lorsque son dénominateur est non nul. Donc ici, il y a des valeurs interdites; et il faut déterminer le domaine d'étude.
On doit avoir: $3x-1≠0$
Soit: $x≠{1}/{3}$. Donc $\D_E=ℝ\\\{{1}/{3}\}$
(E3) $⇔$ ${-x+2}/{3x-1}=0$ ((E3) n'est pas une équation du premier degré; le membre de droite est nul, et le membre de gauche est un quotient).
Un quotient est nul lorsque son numérateur est nul.
(E3) $⇔$ $-x+2=0$ (on s'est ramené à une équation du premier degré)
(E3) $⇔$ $x=2$ (cette valeur n'est pas interdite)
Donc $\S=\{\,2\,\}$
Equation (E4)
(E4) $⇔$ $x^2-x=0$ ((E4) n'est pas une équation du premier degré; on factorise).
(E4) $⇔$ $x(x-1)=0$
(E4) $⇔$ $x=0$ ou $x-1=0$ (on s'est ramené à deux équations du premier degré).
(E4) $⇔$ $x=0$ ou $x=1$
Donc $\S=\{\,0\,;\,1\,\}$
Equation (E5)
(E5) $⇔$ $x^2+6x+9=0$ ((E5) n'est pas une équation du premier degré; on factorise).
(E5) $⇔$ $(x+3)^2=0$
(E5) $⇔$ $x+3=0$ ou $x+3=0$ (on s'est ramené à deux équations du premier degré semblables).
(E5) $⇔$ $x=-3$
Donc $\S=\{\,-3\,\}$
Partie B
Rappel: si les 2 membres d'une inéquation sont multipliés ou divisés par un nombre strictement négatif, alors le sens de l'inégalité change!
(In1) $⇔$ $2x+1≤0$
(In1) $⇔$ $2x≤-1$
(In1) $⇔$ $x≤{-1}/{2}$
Donc $\S=]\,-\∞\,;\,{-1}/{2}\,]$
(In2) $⇔$ $-3x+7<0$
(In2) $⇔$ $-3x<-7$
(In2) $⇔$ $x>{-7}/{-3}$
(In2) $⇔$ $x>{7}/{3}$
Donc $\S=]\,{7}/{3}\,;\,+\∞\,[$
(S1) $⇔$ $\{\table x-1>2; -5x<6$
(S1) $⇔$ $\{\table x>2+1; x>{6}/{-5}$
(S1) $⇔$ $\{\table x>3; x>-1.2$
(S1) $⇔$ $x>3$
Donc $\S=]\,3\,;\,+\∞\,]$
(S2) $⇔$ $\{\table 2x-3>4; 5x<35$
(S2) $⇔$ $\{\table 2x>4+3; x<{35}/{5}$
(S2) $⇔$ $\{\table x>{7}/{2}; x<7$
(S2) $⇔$ $\{\table x>3.5; x<7$
(S2) $⇔$ $3,5$<$x$<$7$
Donc $\S=]\,3,5\,;\,7\,[$
(S3)$⇔$ $\{\table 2x+3<x; -2x<6$
(S3)$⇔$ $\{\table 2x-x<-3; x>{6}/{-2}$
(S3)$⇔$ $\{\table x<-3; x>-3$
Donc $\S=∅$