 Algorithmes
Algorithmes
Exercice 2
Les 2 parties sont indépendantes.
Partie A
Le cinéma Kino propose un abonnement. La carte d'abonnement vaut 10 euros. L'abonné paye alors chaque entrée 6,50 euros.
Si un client n'a pas de carte d'abonnement, alors il paye chaque entrée 8,30 euros.
On réalise un programme permettant de savoir le coût total supporté par un client qui serait allé N fois au cinéma.
Le programme distingue 2 cas, suivant que le client a une carte d'abonnement ou non.
Voici l'algorithme associé au programme en question.
Cet algorithme est incomplet.
Afficher "Si le client est abonné, alors taper 1, sinon taper 0"
Lire A
Afficher "Donner le nombre de films vus par le client"
Lire N
P ← 0
Si A = ...
Alors
P ← N x 8,30
Sinon
P ← ...
Fin du Si
Afficher "La somme totale payée par le client s'élève à "
Afficher ...
Afficher "euros"
1. Quelle est la somme totale payée par un client sans abonnement ayant vu 5 films ?
2. Quelle est la somme totale payée par un client avec abonnement ayant vu 12 films ?
3. Compléter l'algorithme proposé ?
4. Voici un programme en PYTHON correspondant à l'algorithme proposé. Compléter les lignes 3, 4, 5, 6 et 8 pour que ce programme fonctionne correctement.
1. A=int(input("Si le client est abonné, alors taper 1, sinon taper 0"))
2. N=int(input("Donner le nombre de films vus par le client"))
3.
4. if A
5. P=
6.
7. P=N
8. print("La somme totale payée par le client s'élève à ",
Partie B
Le cinéma Movy propose un système d'abonnement gratuit. Un abonné paye chacune de ses 8 premières séances 10 euros.
Mais à partir de la 9ème, la séance ne vaut plus que 5 euros.
1. Quelle est la somme totale payée par un abonné ayant vu 8 films ?
2. Quelle est la somme totale payée par un abonné ayant vu 12 films ?
3. Ecrire l'algorithme d'un programme permettant de savoir le coût total supporté par un abonné qui serait allé N fois au cinéma.
4. Ecrire un programme en Python correspondant à l'algorithme précédent.
Corrigé
Partie A
1. On a: 5 x 8,30 = 41,50
Donc la somme totale payée par un client sans abonnement ayant vu 5 films est de 41,50 euros.
2. On a: 12 x 6,50+ 10 = 88
Donc la somme totale payée par un client avec abonnement ayant vu 12 films est de 88 euros.
3. Voici l'algorithme complété
Afficher "Si le client est abonné, alors taper 1, sinon taper 0"
Lire A
Afficher "Donner le nombre de films vus par le client"
Lire N
P ← 0
Si A = 0
Alors
P ← N x 8,30
Sinon
P ← N x 6,50 + 10
Fin du Si
Afficher "La somme totale payée par le client s'élève à "
Afficher P
Afficher "euros"
Le fonctionnement du programme, non demandé, est donné ci-dessous:
Par exemple, pour un client sans abonnement ayant vu 5 films.
Il s'affiche "Si le client est abonné, alors taper 1, sinon taper 0"
L'utilisateur tape donc 0. Par conséquent: A=0.
Il s'affiche "Donner le nombre de films vus par le client"
L'utilisateur tape donc 5. Par conséquent: N=5.
P=0
Comme on a: A = 0, on passe au Alors.
P=5x8,30=41,50
Il s'affiche "La somme totale payée par le client s'élève à 41,50 euros"
Par exemple, pour un client avec abonnement ayant vu 12 films.
Il s'affiche "Si le client est abonné, alors taper 1, sinon taper 0"
L'utilisateur tape donc 1. Par conséquent: A=1.
Il s'affiche "Donner le nombre de films vus par le client"
L'utilisateur tape donc 12. Par conséquent: N=12.
P=0
Comme on n'a pas: A = 0, on passe au Sinon.
P=12x6,50+10=88
Il s'affiche "La somme totale payée par le client s'élève à 88 euros"
4. Voici le programme en PYTHON complété.
1. A=int(input("Si le client est abonné, alors taper 1, sinon taper 0"))
2. N=int(input("Donner le nombre de films vus par le client"))
3. P=0
4. if A ==0 :
5. P= N * 8,30
6. else:
7. P=N * 6,50 + 10
8. print("La somme totale payée par le client s'élève à ",P,"euros")
L'exécution de la procedure input de la ligne 1 provoque l'apparition d'une fenêtre de saisie avec le texte "Si le client est abonné, alors taper 1, sinon taper 0".
Le nombre entré par l'utilisateur sera affecté à la variable A. Mais tout ce qui est saisi par l'utilisateur est considéré par PYTHON comme étant une chaîne de caractères.
Pour que PYTHON comprenne que le 0 ou le 1 est bien un entier, on utilise la méthode int, qui transforme le texte saisi par l'utilisateur en nombre.
Par ailleurs, on notera le double = pour tester si A vaut 0. Un égal simple aurait affecté à A la valeur 0 sans faire de test!
Partie B
1. On a: 8 x 10 = 80
Donc la somme totale payée par un abonné ayant vu 8 films est de 80 euros.
2. On a: 80 + ( 12 - 8 ) x 5 = 100
Donc la somme totale payée par un abonné ayant vu 12 films est de 100 euros.
3. Voici un algorithme convenable.
Afficher "Donner le nombre de films vus par le client"
Lire N
P ← 0
Si N < 9
Alors
P ← N x 10
Sinon
P ← 80 + ( N - 8 ) x 5
Fin du Si
Afficher "La somme totale payée par l'abonné s'élève à "
Afficher P
Afficher "euros"
4. Voici un programme correct.
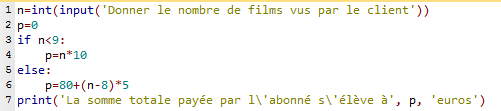
Dans la ligne 1, la méthode int() transforme la chaîne saisie n en un entier n
. Sans cela, le programme ne peut pas comparer la variable n à l'entier 9 dans la suite du programme.
Dans la ligne 7, noter la différence entre l'affichage d'un texte (entre quotes) et l'affichage d'une variable (sans quote).
De plus, on retiendra que, pour afficher une apostrophe (ou quote), on le fait précéder d'un antislash \