 Algorithmes
Algorithmes
Exercice 4
RAPPELS POUR LES DEBUTANTS
L'instruction Pour $I$ allant de 0 à $N-1$ est le début d'une boucle.
Les instructions qui se trouvent entre Pour $I$ allant de 0 à $N-1$ et Fin du Pour seront répétées.
Dans l'algorithme ci-dessous, il n'y a qu'une seule instruction à répéter, qui est $U$ ← $0,95×U$
A la première boucle, la variable $I$ vaudra 0, puis, à chaque nouvelle boucle, la variable $I$ sera automatiquement augmentée de 1.
A la dernière boucle, $I$ vaudra $N-1$.
On considère un programme associé à l'algorithme suivant:
Lire $N$
$U$ ← 1000
Pour $I$ allant de 0 à $N-1$
$U$ ← $0,95×U$
Fin du Pour
Afficher $U$
1. Donner les valeurs successives prises par $I$ et $U$ lorsque le programme fonctionne pour une valeur de $N$ égale à 2.
Que s'affiche-t-il à la fin?
2. Compléter les lignes 3 et 4 du programme suivant (écrit en Python) pour qu'il soit conforme à l'algorithme proposé.
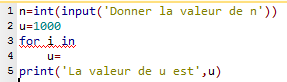
3. Une citerne contient 1000 litres d'eau. Chaque jour, 5% de l'eau s'évapore.
Quel serait l'intérêt d'un tel algorithme dans ce cas?
4. Ecrire un algorithme donnant le même résultat que celui donné au début de l'énoncé, mais en remplaçant la boucle Pour par une boucle Tant
que.
5. Supprimer une ligne de l'algorithme précédent, puis en modifier deux lignes pour que le nouvel algorithme permette de déterminer au bout de combien de
jours la citerne contiendra moins de 900 litres.
6. Compléter ou modifier les lignes 1, 3 et 6 du programme suivant (écrit en Python) pour qu'il soit conforme à l'algorithme proposé à la question 5.
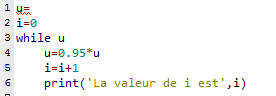
Corrigé
1. $N=2$; $U=1000$.
On note que $N-1=2-1=1$.
La boucle sera répétée pour I variant de 0 à 1.
$I=0$: Première boucle
$U=0,95×1000=950$.
Fin de la première boucle.
$I=1$: Seconde boucle
$U=0,95×950=902,5$.
Fin de la seconde boucle.
Il n'y a pas de troisième boucle car I variait de 0 à 1 dans les boucles, et il a atteint 1 à la fin de la dernière boucle.
Finalement, il s'affiche la valeur de $U$, c'est à dire 902,5.
2. Voici un programme correct.
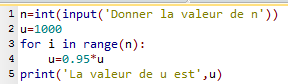
La ligne 3 marque le début d'une boucle for, qui ne contient que la ligne 4.
Dans la ligne 3, range(n) est une liste contenant les entiers de 0 à n-1.
A la première boucle, i vaudra 0. A la seconde boucle, i vaudra 1.
...etc...
A la dernière boucle, i vaudra n-1.
Ainsi, la boucle sera effectuée n fois.
Attention! Ne pas oublier le : en bout de la ligne 3!
Remarquer que l'indentation cesse à la ligne 5 qui ne fait pas partie de la boucle.
3. Si chaque jour, 5% de l'eau s'évapore, alors il en reste 95%.
Et par là, si U est la quantité restant dans la citerne un jour donné,
alors la quantité qui reste le lendemain vaut $0,95×U$.
Le programme proposé demande donc à l'utilisateur de saisir une valeur $N$ qui correspond à un nombre de jours.
Puis il affiche la quantité d'eau restant dans la citerne au bout de ces N jours.
Par exemple, au bout de 2 jours (N=2), le programme renvoie une valeur égale à 902,5, c'est à dire qu'il reste 902,5 litres d'eau dans la citerne au bout de 2
jours.
4. Algorithme équivalent à celui du début:
Lire $N$
$U$ ← 1000
$I$ ← 0
Tant que $I$<$N$
$U$ ← $0,95×U$
$I$ ← $I+$1
Fin du Tant que
Afficher $U$
(Noter que, cette fois ci, il est indispensable d'augmenter $I$ de 1, car l'incrémentation n'est pas automatique à la fin d'une boucle du type Tant que)
5. Nouvel algorithme:
(Noter que la ligne Lire $N$ a disparu)
$U$ ← 1000
$I$ ← 0
Tant que $U≥900$ (Noter le $U≥900$ à la place de $I$<$N$)
$U$ ← $0,95×U$
$I$ ← $I+$1
Fin du Tant que
Afficher $I$ (Noter le $I$ à la place de $U$)
6. Voici un programme correct.
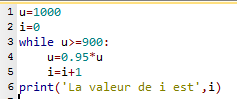
La ligne 1 permet d'affecter la valeur 1000 à la variable u.
La ligne 3 marque le début d'une boucle while, qui contient les lignes 4 et 5.
On ne sait pas d'avance combien de fois cette boucle sera effectuée.
Elle sera répétée tant que u reste supérieur ou égal à 900.
Attention! Ne pas oublier le : en bout de la ligne 3!
La ligne 6 ne fait pas partie de la boucle; par conséquent, elle n'et pas indentée (il n'y a plus de décalage vers la droite).
Remarque: si l'on fait fonctionner ce programme, il s'affichera finalement "La valeur de i est 3" (car $u_3=857,375$ est la première valeur de $u_n$ en dessous de 900).
Finalement, la citerne contient moins de 900 litres au bout de 3 jours.