Algorithmes
Exercice 5
Julie fait tourner une roue comportant 3 secteurs angulaires numérotés de 1 à 3.
Quand la roue a terminé de tourner, seul un secteur reste visible.
Pour k entier entre 1 et 3, on note:
k: "le secteur k reste visible"
On a: $p(1)=0,2$ $p(2)=0,5$
1. Déterminer $p(3)$.
2. Le programme ci-dessous, écrit en PYTHON, simule un unique lancer de roue et affiche dans la console une phrase du type:
le secteur k est sorti
(où k est un entier entre 1 et 3).
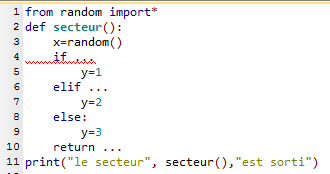
On rappelle que la fonction random() retourne un nombre (à virgule) aléatoire entre 0 et 1.
Recopier et compléter les lignes 4, 6 et 10 pour que le programme fonctionne correctement.
3.
Supprimer la ligne 11 du programme précédent,
puis compléter le programme en définissant une nouvelle fonction, appelée simul(n)
qui simule n lancers de la roue, et affiche n fois de suite une phrase du type
le secteur k est sorti
(où k est un entier entre 1 et 3).
Corrigé
1. On a: $p(1)+p(2)+p(3)=1$
Soit: $0,2+0,5+p(3)=1$
Et donc: $p(3)=1-0,2-0,5$
Soit: $p(3)=0,3$
2. Voici le programme corrigé:
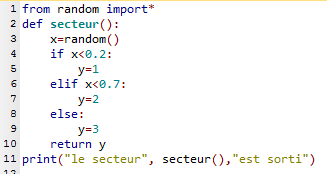
x est un nombre (à virgule) aléatoire entre 0 et 1.
La probabilité pour que x soit plus petit que 0,2 est évidemment égale à 0,2.
Et comme $0,2+0,5=0,7$, alors la probabilité pour que x soit compris entre 0,2 et 0,7 est égale à 0,5.
Et enfin, la probabilité pour que x soit compris entre 0,7 et 1 est égale à 0,3.
La valeur de y, qui est le numéro du secteur visible, est retournée par la fonction secteur().
3.Voici un programme convenable:
La variable k va prendre successivement les valeurs 0, 1, 2, 3, ... jusquà n-1. La boucle for sera donc parcourue n fois.
Chaque boucle permet d'afficher une phrase simulant un lancer de roue.
La ligne 15, non demandée, permet d'afficher 4 phrases du type prévu.
J'ai obtenu:
le secteur 2 est sorti
le secteur 3 est sorti
le secteur 1 est sorti
le secteur 2 est sorti
Evidemment, votre résultat sera sans doute différent! C'est le propre d'une expérience aléatoire!