 La géométrie analytique du plan
La géométrie analytique du plan
Exercice 2
Le plan est rapporté à un repère orthonormé (O,I,J).
On considère les points $A(-2;1)$, $B(4;-3)$, $C(6;0)$ et $D(x_D;y_D)$.
Il est conseillé de faire une figure.
1. Que dire du triangle ABC?
2. Soit $K(x_K;y_K)$ le milieu du segment [AC].
Déterminer les coordonnées du point K.
3. Le point $K$ est le milieu du segment [BD].
Déterminer les coordonnées du point D.
4. Démontrer, sans faire aucun calcul supplémentaire, que AC=BD.
Solution...
Corrigé
Un rappel important: une démonstration part toujours de l'énoncé ou de ce qui a déjà été prouvé auparavant.
Vous remarquerez donc que, dans ce qui suit, chaque début de réponse est soit une phrase de l'énoncé, soit un résultat prouvé antérieurement.
La figure non demandée est tracée ci-dessous.
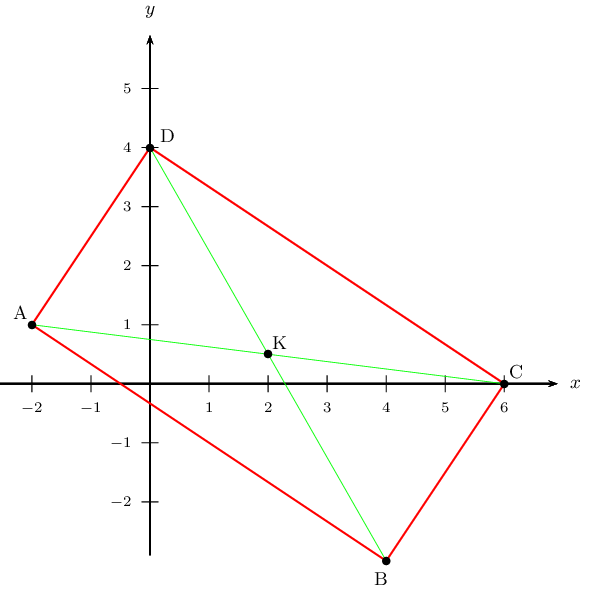
1. A savoir ici: la formule donnant la distance entre 2 points (dans un repère orthonormé).
Le plan est rapporté à un repère orthonormé (O,I,J).
On considère les points $A(-2;1)$, $B(4;-3)$, $C(6;0)$ et $D(x_D;y_D)$.
Nous allons démontrer que le triangle ABC est rectangle en B en utilisant la réciproque du théorème de Pythagore.
On a: $AB=√{(x_B-x_A)^2+(y_B-y_A)^2}$
Soit: $AB=√{(4-(-2))^2+(-3-1)^2}=√{6^2+(-4)^2}=√{36+16}=√{52}$
De même, on a: $BC=√{(x_C-x_B)^2+(y_C-y_B)^2}$
Soit: $BC=√{(6-4)^2+(0-(-3))^2}=√{2^2+3^2}=√13$
De même, on a: $AC=√{(x_C-x_A)^2+(y_C-y_A)^2}$
Soit: $AC=√{(6-(-2))^2+(0-1)^2}=√{8^2+(-1)^2}=√65$
On calcule alors: $AB^2+BC^2=52+13=65$.
Or: $AC^2=65$.
Donc: $AB^2+BC^2=AC^2$.
Donc ABC est rectangle en B.
2. A savoir ici: la formule donnant les coordonnées du milieu d'un segment.
$K(x_K;y_K)$ est le milieu du segment [AC].
Donc: $x_K={x_A+x_C}/{2}$ et $y_K={y_A+y_C}/{2}$
Soit: $x_K={-2+6}/{2}=2$ et $y_K={1+0}/{2}=0,5$
Donc: $K(2;0,5)$.
3. Le point K est le milieu du segment [BD].
Donc: $x_K={x_B+x_D}/{2}$ et $y_K={y_B+y_D}/{2}$
Soit: $2={4+x_D}/{2}$ et $0,5={-3+y_D}/{2}$
Donc: $2 ×2=4+x_D$ et $0,5×2=-3+y_D$
Donc: $4-4=x_D$ et $1+3=y_D$
Soit: $0=x_D$ et $4=y_D$
Donc: $D(0;4)$.
4.
Nous savons que le point K est le milieu des segments [AC] et [BD].
Donc le quadrilatère ABCD possède des diagonales ayant le même milieu.
Donc ABCD est un parallélogramme.
Or le triangle ABC est rectangle en B.
Donc le parallélogramme ABCD possède 2 côtés consécutifs perpendiculaires.
Donc le parallélogramme ABCD est un rectangle.
Donc ses diagonales [AC] et [BD] ont la même longueur.
Donc AC=BD.
A retenir:
Pour montrer qu'un quadrilatère est un parallélogramme, il suffit de montrer que ses diagonales ont le même milieu.
Pour montrer qu'un quadrilatère est un rectangle, il suffit de montrer que c'est un parallélogramme, et qu'il possède 2 côtés consécutifs perpendiculaires.