 La fonction carré
La fonction carré
Exercice 1
- Résoudre l'équation (1): $2x^2-18=0$.
- Résoudre l'équation (2): $5(x+2)^2-80=0$.
- Résoudre l'équation (3): $x^2+3x-6=-1+3x$.
- Résoudre l'équation (4): $(2x-1)(x^2-10)=0$.
- Résoudre l'équation (5): $x^2+3=0$.
- Résoudre l'inéquation (6): $x^2<9$.
- Résoudre l'inéquation (7): $x^2>9$.
- Résoudre l'inéquation (8): $-3x^2≤-11$.
- Résoudre l'inéquation (9): $x^2+1≥0$.
Solution...
Corrigé
A retenir: dans une équation ou une inéquation dont le membre de droite est nul,
si le membre de gauche contient des $x$ uniquement dans un carré,
alors il est conseillé d'isoler ce carré.
- (1) $⇔$ $2x^2-18=0$ $⇔$ $2x^2=18$ $⇔$ $x^2={18}/{2}$ $⇔$ $x^2=9$
On a isolé le carré.
On obtient donc: (1) $⇔$ $x=√9$ ou $x=-√9$
Donc: (1) $⇔$ $x=3$ ou $x=-3$
S$=\{-3;3\}$
A retenir: si $a≥0$, alors: $x^2=a$ $⇔$ $x=√a$ ou $x=-√a$. - (2) $⇔$ $5(x+2)^2-80=0$ $⇔$ $5(x+2)^2=80$ $⇔$ $(x+2)^2={80}/{5}$ $⇔$ $(x+2)^2=16$
On a isolé le carré.
On obtient donc: (2) $⇔$ $x+2=√{16}$ ou $x+2=-√{16}$
Donc: (2) $⇔$ $x=4-2=2$ ou $x=-4-2=-6$
S$=\{-6;2\}$
A retenir: si $a≥0$, alors: $x^2=a$ $⇔$ $x=√a$ ou $x=-√a$. - (3) $⇔$ $x^2+3x-6=-1+3x$ $⇔$ $x^2+3x-6+1-3x=0$ $⇔$ $x^2-5=0$ $⇔$ $x^2=5$
Donc: (3) $⇔$ $x=√5$ ou $x=-√5$
S$=\{-√5;√5\}$ - (4) $⇔$ $(2x-1)(x^2-10)=0$ $⇔$ $2x-1=0$ ou $x^2-10=0$.
A retenir: un produit de facteurs est nul si et seulement si l'un d'eux est nul.
On continue donc: (4) $⇔$ $x={1}/{2}$ ou $x^2=10$
Et donc: (4) $⇔$ $x=0,5$ ou $x=-√{10}$ ou $x=√{10}$
S$=\{-√{10};0,5;√{10}\}$ - (5)$⇔$ $x^2+3=0$ $⇔$ $x^2=-3$
Or, un carré est positif ou nul. Donc l'égalité $x^2=-3$ est absurde.
Donc l'équation (5) n'a pas de solution.
S$= ∅$ - Pour résoudre une telle inéquation, il faut avoir en tête l'allure de la parabole représentant la fonction carré
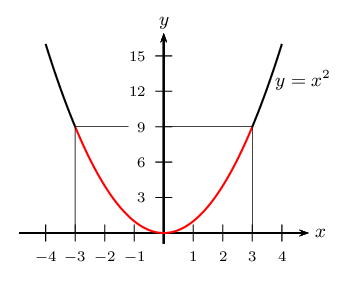
(6) $⇔$ $x^2 < 9$ $⇔$ $-√{9}$<$x$<$√{9}$
Soit: (6) $⇔$ $-3$<$x$<$3$
S$=]-3;3[$
A retenir: si $a≥0$, alors: $x^2$<$a$ $⇔$ $-√{a}$<$x$<$√{a}$. - Pour résoudre une telle inéquation, il faut avoir en tête l'allure de la parabole représentant la fonction carré (voir inéquation (6))
(7) $⇔$ $x^2>9$ $⇔$ $x$<$-√{9}$ ou $x$>$√{9}$
Soit: (7) $⇔$ $x$<$-3$ ou $x$>$3$
S$=]-\∞;-3$$]∪[$$3;+\∞[$
A retenir: si $a≥0$, alors: $x^2≥a$ $⇔$ $x≤-√{a}$ ou $x≥√{a}$. - (8) $⇔$ $-3x^2≤-11$ $⇔$ $x^2≥{-11}/{-3}$
A retenir: une inégalité change de sens si on divise chacun de ses membres par un nombre strictement négatif.
On continue alors: (8) $⇔$ $x^2≥{11}/{3}$ $⇔$ $x≤-√{{11}/{3}}$ ou $x≥√{{11}/{3}}$
S$=]-\∞;-√{{11}/{3}}$$]∪[$$√{{11}/{3}};+\∞[$
A retenir: si $a≥0$, alors: $x^2≥a$ $⇔$ $x≤-√{a}$ ou $x≥√{a}$. - (9) $⇔$ $x^2≥-1$
Or, un carré est positif ou nul. Donc l'inégalité $x^2≥-1$ est toujours vraie.
Donc l'ensemble des solutions de l'inéquation (9) est l'ensemble de tous les réels.
S$=ℝ$