 La fonction carré
La fonction carré
Exercice 6
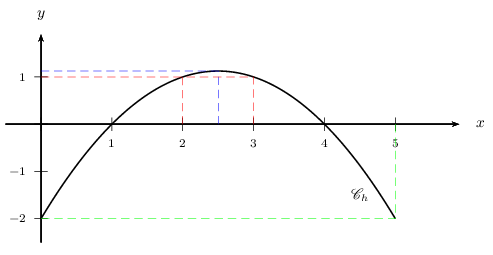
La fonction $h$ définie sur [0;5] est tracée ci-dessous.
-
Résoudre graphiquement l'équation $h(x)=0$.
- Résoudre graphiquement l'inéquation $h(x)>0$.
- Résoudre graphiquement l'équation $h(x)=-2$.
- Résoudre graphiquement l'inéquation $h(x)≤1$.
- On admet désormais que $h(x)=-0,5x^2+2,5x-2$.
Montrer que $h(x)=(-0,5x+2)(x-1)$.
 Retrouver algébriquement les 3 premiers résultats précédents.
Retrouver algébriquement les 3 premiers résultats précédents.
 Montrer que $h(x)=-0,5(x-2,5)^2+1,125$, puis retrouver algébriquement les solutions de l'inéquation de la question 4.
Montrer que $h(x)=-0,5(x-2,5)^2+1,125$, puis retrouver algébriquement les solutions de l'inéquation de la question 4.
Corrigé

- $h(x)=0$ $⇔$ $x=1$ ou $x=4$
S$=\{1;4\}$ -
$h(x)>0$ $⇔$ $1$<$x$<$4$.
S$=]1;4[$ -
$h(x)=-2$ $⇔$ $x=0$ ou $x=5$
S$=\{0;5\}$ -
$h(x)≤1$ $⇔$ $x≤2$ ou $x≥3$
Et comme on résout sur [0;5], on obtient:
S$=[0;2[∪]3;5]$ - On a: $(-0,5x+2)(x-1)=-0,5x^2+0,5x+2x-2=-0,5x^2+2,5x-2=h(x)$.
On a bien montré que $h(x)=(-0,5x+2)(x-1)$.
A retenir:
$h(x)$ apparaît sous 2 formes possibles: une forme factorisée, et une forme développée.
Il conviendra de choisir la plus adaptée en fonction de la question posée.
Retrouvons le premier résultat.
$h(x)=0$ $⇔$ $(-0,5x+2)(x-1)=0$ $⇔$ $-0,5x+2=0$ ou $x-1=0$ $⇔$ $x={-2}/{-0,5}=4$ ou $x=1$
S$=\{1;4\}$
A retenir: un produit de facteurs est nul si et seulement si l'un d'eux est nul.
Cette propriété nous a insité à choisir la forme factorisée de $h$.
Retrouvons le second résultat.
$h(x)>0$ $⇔$ $(-0,5x+2)(x-1)$>$0$
Le membre de gauche est un produit $p$ dont nous allons tout d'abord trouver le signe.
$-0,5x+2$ est une fonction affine s'annulant pour $x=4$.
De plus, son coefficient directeur est strictement négatif (il vaut $-0,5$).
$x-1$ est une fonction affine s'annulant pour $x=1$.
De plus, son coefficient directeur est strictement positif (il vaut 1).
D'où le tableau de signes du produit $p$.
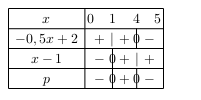
Or, on cherche pour quels $x$ ce produit $p$ est strictement positif.
Donc: S$=]1;4[$
A retenir: pour dresser le tableau de signes d'une fonction affine (non constante), il suffit de repérer pour quelle valeur elle s'annule. A droite de cette valeur, elle est du signe de son coefficient directeur.
Retrouvons le troisième résultat.
A savoir: dans une équation, il est conseillé de commencer par rendre le membre de droite égal à 0.
Puis, si le membre de gauche n'est pas une fonction affine, alors il est souvent conseillé d'essayer soit de le factoriser, soit de réduire les termes au même dénominateur.
Ici, nous allons factoriser (après avoir réduit).
$h(x)=-2$ $⇔$ $-0,5x^2+2,5x-2=-2$ $⇔$ $-0,5x^2+2,5x-2+2=0$
Remarque: la présence du $-2$ à droite nous a insité à choisir la forme développée de $h(x)$.
On obtient alors: $h(x)=-2$ $⇔$ $-0,5x^2+2,5x=0$
Soit: $h(x)=-2$ $⇔$ $x(-0,5x+2,5)=0$ $⇔$ $x=0$ ou $-0,5x+2,5=0$ $⇔$ $x=0$ ou $x=5$
S$=\{0;5\}$
Retrouvons le quatrième résultat.
Montrons tout d'abord l'égalité proposée.
On a: $-0,5(x-2,5)^2+1,125=-0,5(x^2-2×x×2,5+2,5^2)+1,125=-0,5x^2+2,5x-3,125+1,125-0,5x^2+2,5x-2=h(x)$
On a bien montré que $h(x)=-0,5(x-2,5)^2+1,125$.
Reprenons l'inéquation de la question 4.
$h(x)≤1$ $⇔$ $-0,5(x-2,5)^2+1,125≤1$
Remarque: la forme de $h(x)$ choisie permet d'isoler le carré dans lequel apparaît $x$.
On a : $h(x)≤1$ $⇔$ $-0,5(x-2,5)^2≤1-1,125$
Soit : $h(x)≤1$ $⇔$ $(x-2,5)^2≥{-0,125}/{-0,5}$
Remarque: diviser chaque membre par le nombre strictement négatif $-0,5$ change le sens de l'inégalité.
On a donc: $h(x)≤1$ $⇔$ $(x-2,5)^2≥0,25$
Remarque: pour résoudre une telle inéquation, il faut avoir en tête l'allure de la parabole représentant la fonction carré
On obtient donc: $h(x)≤1$ $⇔$ $x-2,5≤-√{0,25}$ ou $x-2,5≥√{0,25}$
Soit: $h(x)≤1$ $⇔$ $x-2,5≤-0,5$ ou $x-2,5≥0,5$
Et donc: $h(x)≤1$ $⇔$ $x≤-0,5+2,5$ ou $x≥0,5+2,5$
Soit: $h(x)≤1$ $⇔$ $x≤2$ ou $x≥3$
Et comme on résout sur [0;5], on obtient:
S$=[0;2[∪]3;5]$