Corrigé

1. $M(x;y)∈(AB)$ $⇔$ ${AM}↖{→}$ et ${AB}↖{→}$ sont colinéaires.
Or ${AM}↖{→}$ a pour coordonnées: $(x-1;y-2)$.
Et ${AB}↖{→}$ a pour coordonnées: $(4-1;0-2)=(3;-2)$.
Donc: $M(x;y)∈(AB)$ $⇔$ $(x-1)×(-2)-3×(y-2)=0$ (le déterminant des 2 vecteurs colinéaires est nul)
Donc: $M(x;y)∈(AB)$ $⇔$ $-2x+2-3y+6=0$
Donc: $M(x;y)∈(AB)$ $⇔$ $-2x-3y+8=0$
Ceci est une équation cartésienne de la droite (AB).
A retenir: la méthode utilisant la colinéarité de vecteurs pour obtenir facilement une équation de droite.

2. Le vecteur ${u}↖{→}(2;0,5)$ est directeur de la droite $d_1$.
Si on pose: $-b=2$ et $a=0,5$, c'est à dire: $b=-2$ et $a=0,5$, alors $d_1$ admet une équation cartésienne du type: $ax+by+c=0$.
Donc $d_1$ admet une équation cartésienne du type:: $0,5x-2y+c=0$.
A retenir: la droite de vecteur directeur ${u}↖{→}(-b;a)$ admet une équation cartésienne du type: $ax+by+c=0$. Or $d_1$ passe par $A(1;2)$.
Donc: $0,5×1-2×2+c=0$.
Donc: $c=3,5$.
Donc $d_1$ admet pour équation cartésienne: $0,5x-2y+3,5=0$.
Or: $0,5x-2y+3,5=0$ $⇔$ $-2y=-0,5x-3,5$ $⇔$ $y={-0,5x-3,5}/{-2}$ $⇔$ $y=0,25x+1,75$
Donc $d_1$ admet pour équation réduite: $y=0,25x+1,75$.

3. La droite $d_2$ passant par A et de pente $-2$ admet une équation du type: $y=-2x+b$
Or $d_2$ passe par $A(1;2)$. Donc: $2=-2×1+b$.
Donc: $4=b$.
Donc $d_2$ admet pour équation réduite: $y=-2x+4$.

4. $d_2$ admet pour équation réduite: $y=-2x+4$.
Donc elle admet pour vecteur directeur ${v}↖{→}(1;-2)$
("on avance de 1 vers la droite, puis on descend de 2")

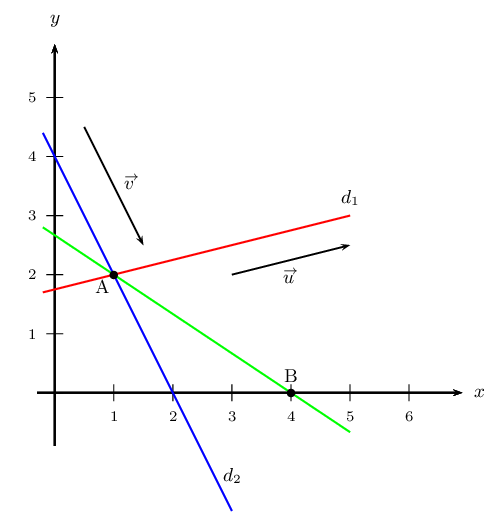
5. Voici la figure demandée.