Corrigé

1. La droite $d_1$ d'équation $y={2}/{3}x+{1}/{3}$ passe par $A(0;{1}/{3})$ et son coefficient directeur vaut ${2}/{3}$.
La droite $d_2$ d'équation $y=-{1}/{2}x+5$ passe par $C(0;5)$ et son coefficient directeur vaut $-{1}/{2}$.
D'où les tracés suivants:


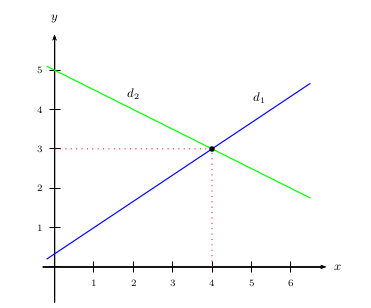
2. Graphiquement, on constate que $d_1$ et $d_2$ se coupent au point de coordonnées $(4;3)$.
Donc la solution du système est le couple $(x;y)=(4;3)$.

3. Les droites associées au système ont des coefficients directeurs différents, donc elles ne sont pas parallèles, et par là, elles sont sécantes en un unique point. Donc le système a bien une solution unique.

Résolution:
Nous allons procéder par substitutions.
$\{\table y={2}/{3}x+{1}/{3}; y=-{1}/{2}x+5$ $⇔$ $\{\table y={2}/{3}x+{1}/{3}; {2}/{3}x+{1}/{3}=-{1}/{2}x+5$
          $⇔$ $\{\table y={2}/{3}x+{1}/{3}; {2}/{3}x+{1}/{2}x=5-{1}/{3}$
          $⇔$ $\{\table y={2}/{3}x+{1}/{3}; {4}/{6}x+{3}/{6}x={15}/{3}-{1}/{3}$
          $⇔$ $\{\table y={2}/{3}x+{1}/{3}; {7}/{6}x={14}/{3}$
          $⇔$ $\{\table y={2}/{3}x+{1}/{3}; x={14}/{3}×{6}/{7}=4$
          $⇔$ $\{\table y={2}/{3}×4+{1}/{3}=3; x=4$
Donc la solution du système est le couple $(x;y)=(4;3)$.