Corrigé

1. Méthode 1: A savoir: une égalité du type $ax+by+c=0$ (avec $a$ et $b$ non tous les deux nuls) est une équation cartésienne de droite.
Il est facile d'en trouver 2 points en remplaçant, par exemple, $x$ par 0 pour l'un, et $y$ par 0 pour l'autre.
La première ligne est associée à la droite $d_1$ passant par les points $A(0;2)$ et $B(8;0)$.
Ici, pour trouver A, on a écrit: $0+4y-8=0$, ce qui a donné: $y=2$.
Et pour trouver B, on a écrit: $x+4×0-8=0$, ce qui a donné: $x=8$.
De même, la seconde ligne est associée à la droite $d_2$ passant par les points $C(0;-{1}/{3})$ et $D(1;0)$.

D'où les tracés suivants:


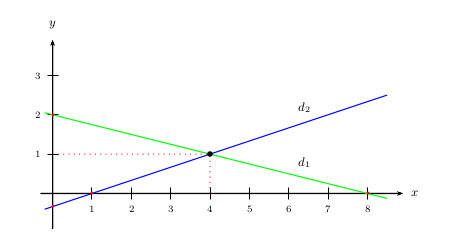
Méthode 2: Cette méthode consiste à retrouver les équations réduites des droites associées à chaque ligne.
$\{\table x+4y-8=0; x-3y-1=0$ $⇔$ $\{\table 4y=-x+8; -3y=-x+1$ $⇔$ $\{\table y=-{1}/{4}x+2; y={1}/{3}x-{1}/{3}$
La droite $d_1$ d'équation $y=-{1}/{4}x+2$ passe par $A(0;2)$ et son coefficient directeur vaut $-{1}/{4}$.
La droite $d_2$ d'équation $y={1}/{3}x-{1}/{3}$ passe par $C(0;-{1}/{3})$ et son coefficient directeur vaut ${1}/{3}$.
On retrouve les tracés obtenus avec la première méthode.

2. Graphiquement, on constate que $d_1$ et $d_2$ se coupent au point de coordonnées $(4;1)$.
Donc la solution du système est le couple $(x;y)=(4;1)$.

3. A savoir: dans un système du type: $\{\table ax+by+c=0; a'x+b'y+c'=0$   , on calcule: $ab'-a'b$.
Si $ab'-a'b≠0$, alors le système admet un couple solution unique.
Sinon, soit il n'admet aucune solution, soit il en admet une infinité.
Avec les notations usuelles, on a: $a=1$, $b=4$, $a'=1$ et $b'=-3$.
On calcule: $ab'-a'b=1×(-3)-1×4=-7$. On a donc: $ab'-a'b≠0$.
Donc le système a bien une solution unique.

Résolution:
Méthode 1: Nous allons procéder par combinaisons linéaires.
$\{\table x+4y-8=0; x-3y-1=0$ $⇔$ $\{\table x+4y-8=0\;\;\;(L_1); x-3y-1=0\;\;\;(L_2)$
          $⇔$ $\{\table x+4y-8=0\;\;\; (L_1); x-3y-1-x-4y+8=0-0\;\;\; (L_2-L_1 ⇨L_2)$
         $⇔$ $\{\table x+4y-8=0\;\;\; (L_1); -7y+7=0 \;\;\;(L_2)$
          $⇔$ $\{\table x+4y-8=0; y=1$
          $⇔$ $\{\table x+4×1-8=0 ; y=1 $
          $⇔$ $\{\table x=4 ; y=1 $
Donc la solution du système est le couple $(x;y)=(4;1)$.

Méthode 2: Nous allons procéder par substitutions.
$\{\table x+4y-8=0; x-3y-1=0$ $⇔$ $\{\table y=-{1}/{4}x+2; y={1}/{3}x-{1}/{3}$
          $⇔$ $\{\table y=-{1}/{4}x+2; -{1}/{4}x+2={1}/{3}x-{1}/{3}$
          $⇔$ $\{\table y=-{1}/{4}x+2; -{1}/{4}x-{1}/{3}x=-{1}/{3}-2$
          $⇔$ $\{\table y=-{1}/{4}x+2; -{3}/{12}x-{4}/{12}x=-{1}/{3}-{6}/{3}$
          $⇔$ $\{\table y=-{1}/{4}x+2; -{7}/{12}x=-{7}/{3}$
          $⇔$ $\{\table y=-{1}/{4}x+2; x=-{7}/{3}×(-{12}/{7})=4$
          $⇔$ $\{\table y=-{1}/{4}×4+2=1; x=4$
Donc la solution du système est le couple $(x;y)=(4;1)$.