Généralités sur les fonctions
Exercice 3
1.a. Dresser le tableau de variation des fonctions $f$ et $g$ tracées ci-dessous.
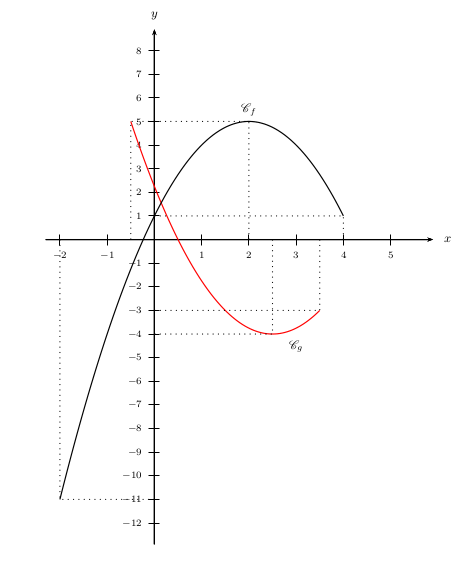
1.b. En vous appuyant sur les tableaux obtenus au 1.a., comparer $f(1,1)$ à $f(1,2)$, puis $g(2,2)$ à $g(2,21)$.
1.c. En vous appuyant sur les tableaux obtenus au 1.a., donner le maximum de chacune des fonctions, puis préciser en quelle valeur il est
atteint.
2.a. La fonction $h$ admet le tableau de variation suivant:
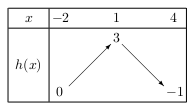
Tracer deux fonctions $h$ possibles.
2.b. Quel est le minimum de $h$?
Quel est le maximum de $h$?
2.c. En vous appuyant sur le tableau de variation de $h$, déterminer le nombre de solutions de chacune des trois équations suivantes:
$h(x)=1,5$, $h(x)=-0,5$, $h(x)=-5$.
Corrigé
1.a. Voici les tableaux de variation demandés.
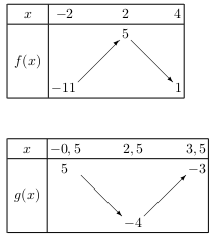
1.b. On sait que $1,1$<$1,2$. Donc $f(1,1)≤f(1,2)$ car la fonction $f$ est croissante entre -2 et 2.
On sait que $2,2$<$2,21$. Donc $g(2,2)≥g(2,21)$ car la fonction $g$ est décroissante entre $-0,5$ et 2,5.
1.c. A retenir: le maximum d'une fonction, s'il existe, est la plus grande de ses images.
Le maximum de $f$ est 5; il est atteint pour $x=2$.
Le maximum de $g$ est 5; il est atteint pour $x=-0,5$.
2.a. Voici les tracés de deux fonctions $h$ possibles.
Remarque: il y a une infinité de courbes possibles associées au tableau de variation proposé!
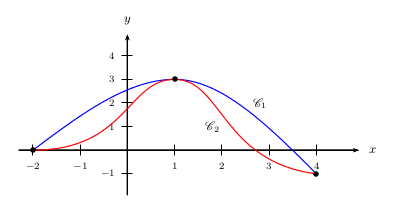
2.b. A retenir: le minimum d'une fonction, s'il existe, est la plus petite de ses images.
le maximum d'une fonction, s'il existe, est la plus grande de ses images.
Le minimum de $h$ est $-1$.
Le maximum de $h$ est 3.
2.c. D'après le tableau de variation donné dans l'énoncé:
$h(x)=1,5$ a 2 solutions. On ne les connaît pas car elles dépendent de la courbe de $h$ choisie!
$h(x)=-0,5$ a 1 solution
$h(x)=-5$ n'a aucune solution.