Généralités sur les fonctions
Exercice 7
On considère la fonction $f$ définie par $f(x)=x^2-2√{x}+2$ sur l'intervalle $[0;4]$.
Cette fonction admet le tableau de variation suivant:
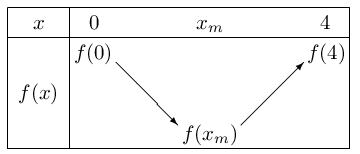
Le programme suivant est écrit en langage Python.
Donner les valeurs successives prises par les variables a, b, milieu, milg et mild.
Il faut être patient! La boucle est parcourue 5 fois!- Quel est l'utilité d'un tel programme?
- A l'aide d'un ordinateur, faites fonctionner ce programme avec delta=0,01. Que s'affiche-t-il à la fin de l'exécution?
Solution...
Corrigé
Pour comprendre la logique de cet algorithme, ne pas hésiter à observer les graphiques en bas de cette page!
-
a=0 b=4 milieu=2 milg=1 mild=3
b-a=4-0=4. Comme b-a>0,2, on commence une première boucle
f(milg)=f(1)=1 f(milieu)=f(2)$≈$3,17
on a: f(milg) < f(milieu)
Cela signifie que $f$ n'est pas décroissante entre milg et milieu; donc $x_m$ est nécessairement entre a et milieu.
b=2 milieu=1
milg=(0+1)/2=0,5 mild=(1+2)/2=1,5
b-a=2-0=2. Comme b-a>0,2, on commence une seconde boucle
f(milg)=f(0,5)$≈$0,84 f(milieu)=f(1)=1
on a: f(milg) < f(milieu)
Cela signifie que $f$ n'est pas décroissante entre milg et milieu; donc $x_m$ est nécessairement entre a et milieu.
b=1 milieu=0,5
milg=(0+0,5)/2=0,25 mild=(0,5+1)/2=0,75
b-a=1-0=1. Comme b-a>0,2, on commence une troisième boucle
f(milg)=f(0,25)$≈$1,06 f(milieu)=f(0,5)$≈$0,84
on n'a pas: f(milg) < f(milieu)
Cela signifie que $f$ n'est pas croissante entre milg et milieu; donc $x_m$ est nécessairement supérieur à milg.
f(mild)=f(0,75)$≈$0,83
on a: f(mild) < f(milieu)
Cela signifie que $f$ n'est pas croissante entre milieu et mild; donc $x_m$ est nécessairement entre milieu et b.
a=0,5 milieu=0,75
milg=(0,5+0,75)/2=0,625 mild=(0,75+1)/2=0,875
b-a=1-0,5=0,5. Comme b-a>0,2, on commence une quatrième boucle
f(milg)=f(0,625)$≈$0,81 f(milieu)=f(0,75)$≈$0,83
on a: f(milg) < f(milieu)
Cela signifie que $f$ n'est pas décroissante entre milg et milieu; donc $x_m$ est nécessairement entre a et milieu.
b=0,75 milieu=0,625
milg=(0,5+0,625)/2=0,5625 mild=(0,625+0,75)/2=0,6875
b-a=0,75-0,5=0,25. Comme b-a>0,2, on commence une cinquième boucle
f(milg)=f(0,5625)$≈$0,816 f(milieu)=f(0,625)$≈$0,809
on n'a pas: f(milg) < f(milieu)
Cela signifie que $f$ n'est pas croissante entre milg et milieu; donc $x_m$ est nécessairement supérieur à milg.
f(mild)=f(0,6875)$≈$0,814
on n'a pas: f(mild) < f(milieu)
Cela signifie que $f$ n'est pas décroissante entre milieu et mild; donc $x_m$ est nécessairement entre milg et mild.
a=0,5625 b=0,6875
milg=(0,5625+0,625)/2=0,59375 mild=(0,625+0,6875)/2=0,65625
b-a=0,6875-0,5625=0,125 Cette fois-ci, on n'a pas b-a>0,2; les boucles s'arrêtent.
Il s'affiche: a=0,5625 b=0,6875
-
D'après le tableau de variation donné, $f$ admet un minimum $f(x_m)$ atteint en $x_m$.
Un tel programme permet de déterminer un encadrement du nombre $x_m$ d'amplitude inférieure ou égale à delta=0,2.
Le nombre $x_m$ est toujours compris entre les valeurs des variables a et b du programme.
$x_m$ est donc compris entre 0,5625 et 0,6875.
Ce programme a procédé par dichotomie, c'est à dire qu'il a divisé l'intervalle de recherche par 2 à chaque boucle.
Pour information, voici graphiquement les valeurs successives des variables sur les 4 premières boucles.
Attention! L'échelle change à chaque graphique.
Variables avant la première boucle:
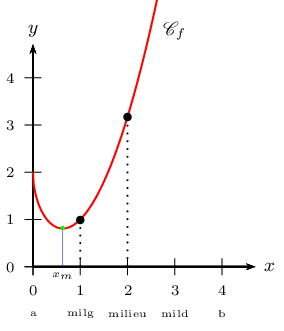
Variables avant la seconde boucle:
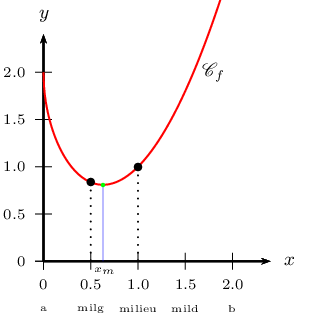
Variables avant la troisième boucle:
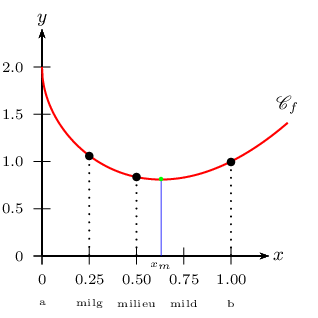
Variables avant la quatrième boucle:
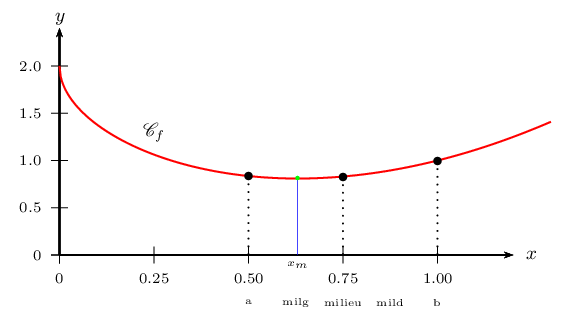
- Si l'on fait fonctionner ce programme à l'aide d'un ordinateur avec delta=0,01, il s'affiche: a=0,625 b=0,6328125
Le nombre $x_m$ est compris entre 0,625 et 0,6328125.
En général, la recherche par dichotomie est plus efficace que la recherche par balayage vue dans l'exercice précédent.