Corrigé

1. On rappelle que les ensembles de nombres remarquables sont inclus les uns dans les autres.
Ainsi, on a:   $ℕ ⊂ ℤ⊂$ 𝔻 $⊂ ℚ⊂ ℝ$ .
Les justifications proposées ci-dessous ne sont pas exigibles.
a.   $-3∈ℤ$    $-3∈\D$    $-3∈ℚ$     $-3∈ℝ$

b. $1.32∈$𝔻    $1.32∈ℚ$     $1.32∈ℝ$

c. $√{7}∈ℝ$     A savoir: si un entier naturel n'est pas un carré d'entier, alors sa racine carrée est réelle.

d. A la calculatrice, on obtient: ${-3}/{11}≈-0,272727...$
Le développement décimal semble illimité de période 27; le nombre semble être rationnel (mais pas décimal). Prouvons le!
Ici, la fraction ${-3}/{11}$ est irréductible, mais le dénominateur 11, qui est un nombre premier (différent de 2 et de 5), ne peut évidemment pas s'écrire sous la forme $ 2^m5^n$.
On a donc: ${-3}/{11}∈ℚ$     ${-3}/{11}∈ℝ$

e. On a: ${13}/{2}=6,5$     Donc: ${13}/{2}∈\D$    ${13}/{2}∈ℚ$     ${13}/{2}∈ℝ$

f. $π∈ℝ$

g. On a: ${√{16}}/{2}=4/2=2$     Donc: ${√{16}}/{2}∈ℕ$     ${√{16}}/{2}∈ℤ$    ${√{16}}/{2}∈$𝔻    ${√{16}}/{2}∈ℚ$     ${√{16}}/{2}∈ℝ$


2. a. 0 est un entier naturel.
b. 8,573 est un nombre décimal.
c. On a: $√81=9$.     Donc $√81$ est un entier naturel.
d. On a: ${1}/{4}=0,25$     Donc ${1}/{4}$ est un nombre décimal.
e. Ici, la fraction ${1}/{3}$ est irréductible, mais le dénominateur 3, qui est un nombre premier (différent de 2 et de 5), ne peut évidemment pas s'écrire sous la forme $ 2^m5^n$.
${1}/{3}$ est donc un nombre rationnel.
f. $√2$ est un nombre réel.
g. On a: $-{3}/{4}=-0,75$     Donc $-{3}/{4}$ est un nombre décimal.
h. Ici, la fraction ${7}/{150}$ est irréductible, mais le dénominateur $150=2×3×5^2$ ne peut évidemment pas s'écrire sous la forme $ 2^m5^n$.
${7}/{150}$ est donc un nombre rationnel.


3. On a: $a= {3}/{7}-{2}/{3}={3×3}/{7×3}-{2×7}/{3×7}={9}/{21}-{14}/{21}=-5/21$
Ici, la fraction est irréductible, mais le dénominateur 21 ne peut pas se décomposer sous la forme $ 2^m5^n$ (en effet : $21=3×7$).
Donc $a$ est donc un nombre rationnel.
Pour se rassurer, on obtient: ${-5}/{21}≈-0,238095238095...$
Le développement décimal semble illimité de période 238095; le nombre semble bien être rationnel (mais pas décimal).

On a: $b=-8×0,125=-1$     Donc $b$ est un entier relatif.

On a: $c={3}/{7}×{2}/{3}={3×2}/{7×3}=6/21=2/7$     Donc, tout comme $a$, $c$ est un nombre rationnel.

On a: $d= √{6}×√{0,24}=√{6×0,24}=√{1,44}=1,2$        Donc $d$ est un nombre décimal.

On a: $e= 1-{1}/{3}=3/3-1/3=2/3$     Donc, tout comme $a$, $e$ est un nombre rationnel.

4. On a: $a=(√{6}+1/√{6})^2=(√{6})^2+2×√{6}×1/√{6}+(1/√{6})^2$
On a utilisé l'identité remarquable: $(a+b)^2=a^2+2ab+b^2$
On obtient ensuite: $a=6+2×1+1^2/(√{6})^2$
On a utilisé les égalités $a×1/a=1$ et $(a/b)^n=a^n/b^n$
On obtient enfin: $a=6+2+1/6=8+1/6=48/6+1/6=49/6$    Ici, la fraction est irréductible, mais le dénominateur 6 ne peut évidemment pas s'écrire sous la forme $ 2^m5^n$.
Donc $a$ est un nombre rationnel.

On a: $b=√{6}×1/√{6}=1$     Donc $b$ est un entier naturel.


5. On a: $x={231}/{60×10^{100}}$
Nous voulons faire apparaitre uniquement des puissances de 10 au dénominateur.
$x={231}/{2^2×3×5×10^{100}}$
Le 3 au dénominateur est imprévu; la fraction doit se simplifier par 3.
$x={77×3}/{2^2×3×5×10^{100}}={77}/{2^2×5×10^{100}}$
Pour faire apparaitre des 10 au dénominateur, il suffit que les exposants de 2 et de 5 soient égaux.
$x={77×5}/{2^2×5^2×10^{100}}={385}/{(2×5)^{2}×10^{100}}={385}/{10^{2}×10^{100}}$
Soit: $x={385}/{10^{102}}$
Donc $x$ est bien un nombre décimal.

6.a. A l'aide de la calculatrice, on obtient $a=1$.
6.b. Le nombre $a$ semble valoir 1; ce serait donc un entier naturel.
Attention! La calculatrice ne manipule qu'une quinzaine de chiffres significatifs, et elle n'en affiche qu'une petite dizaine. Ce que l'on voit à l'écran peut être différent de la valeur exacte!
6.c. Effectuons le calcul du produit:

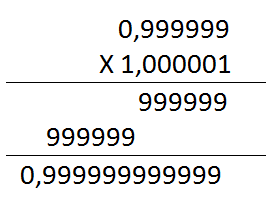
"A la main", on obtient: $a=0,999999999999$. Donc, en réalité, le nombre $a$ est un décimal.
6.d. On calcule: $a=(1+0,000001)×(1-0,000001)$
On utilise l'identité remarquable: $(a+b)(a-b)=a^2-b^2$
On obtient: $a=1^2-0,000001^2=1-(10^{-6})^2=1-10^{-12}=0,999999999999$
On retrouve bien le résultat précédent.