 Nombres et calculs
Nombres et calculs
Exercice 3
1.a. On considère la figure suivante.
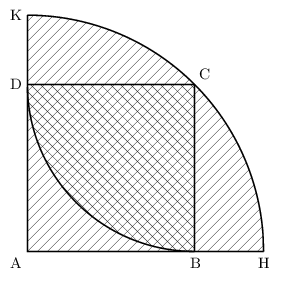
On pose: $x=CB$. ($x$ est évidemment strictement positif)
Exprimer l'aire $a_1$ du carré ABCD en fonction de $x$.
1.b. Exprimer l'aire $a_2$ du quart de disque hachuré en rouge en fonction de $x$.
1.c. Comparer l'aire $a_2$ aux trois quarts de l'aire $a_1$.
1.d.  On appelle $a_3$ l'aire de la surface verte.
On appelle $a_3$ l'aire de la surface verte.
Un logiciel de géométrie nous permet de calculer les aires en fonction de $x$. Par exemple, pour $x=3$, ce logiciel donne pour $a_2$ et pour $a_3$ le même nombre
$7,068583471$.
Peut-on en conclure que, pour tout $x$, les aires $a_2$ et $a_3$ sont égales?
Que peut-on conjecturer?
Prouver votre conjecture.
2. Une question proposée par Maître J.
Dans un triangle, le plus grand des cotés est toujours inférieur à la somme des deux autres cotés (c'est l' "inégalité triangulaire" ).
$x$ désigne ici un nombre réel positif.
On considère un triangle ABC tel que $AB = 7$ , $AC = 2x – 5$ et $BC = x + 2$ .
2.a. Peut-on avoir $x = 3$ ? $x = 15$ ? Justifier dans chaque cas.
2.b. On suppose que le plus grand coté est AB. Montrer que l'inégalité triangulaire donne $x≥{10}/{3}$.
2.c. Reprendre la question précédente si le plus grand coté est AC, puis BC.
2.d. Dans quel intervalle doit se trouver $x$ pour que le triangle ABC existe ?
Solution...
Corrigé
1.a. 
Le carré ABCD admet pour aire $a_1=CB^2=x^2$.
1.b. On rappelle que l'aire d'un disque de rayon $r$ vaut $π × r^2$.
Le quart de disque hachuré en rouge admet pour aire $a_2=1/4 × π × CB^2=π/4 × x^2$
1.c. On doit comparer $a_2=π/4 x^2$ à $3/4 a_1=3/4 x^2$.
Comme $x$ n'est pas nul, cela revient à comparer $π/4$ à $3/4$, c'est à dire $π$ à $3$.
Or on sait que $π$ vaut environ $3,14$, et par là, il est strictement supérieur à 3.
Donc finalement, l'aire $a_2$ est strictement supérieure aux trois quarts de l'aire $a_1$ .
1.d. Les valeurs affichées par le logiciel sont ici approximatives. La seule affirmation correcte est donc que, pour $x=3$, les aires $a_2$ et
$a_3$ sont approximativement égales.
Et même si l'on avait prouvé que les deux aires sont parfaitement égales, cela ne serait vrai que pour $x=3$, et il n'est pas certain que cela restera vrai pour les
autres valeurs de $x$.
Ce que l'on peut faire cependant, c'est conjecturer que, pour tout $x$, les aires $a_2$ et $a_3$ sont égales.
En mathématiques, une conjecture est une hypothèse que l'on n'a pas encore démontrée..
Démontrons donc que cette conjecture est vraie!
L'aire $a_4$ du quart de disque AHK vaut: $a_4=1/4 × π × AC^2$.
Or la diagonale AC du carré ABCD (de côté $x$) vaut $√{2}x$
(On rappelle que la diagonale d'un carré de côté $a$ vaut $√{2} × a$).
Donc on obtient: $a_4=π/4 × (√{2}x)^2=π/4 ×√{2}^2×x^2=2×π/4 × x^2$.
Or l'aire $a_3$ de la surface verte vérifie: $a_3=a_4-a_2$.
Donc $a_3=2×π/4 × x^2-π/4 × x^2=π/4 × x^2$.
Et comme on sait que $a_2=π/4 × x^2$, on obtient: $a_3=a_2$.
L'aire $a_3$ de la surface verte est donc égale à l'aire $a_2$ .
2.
$x$ désigne ici un nombre réel positif.
$AB = 7$ $AC = 2x – 5$ $BC = x + 2$ .
2.a. Si $x = 3$, alors: $AC=1$ et $BC=5$.
On n'a pas: $AC+BC≥AB$. Donc l' inégalité triangulaire n'est pas vérifiée. Ce cas est impossible.
Si $x = 15$, alors: $AC=25$ et $BC=17$.
On n'a pas: $AB+BC≥AC$. Donc l' inégalité triangulaire n'est pas vérifiée. Ce cas est impossible.
2.b. On suppose que le plus grand coté est AB.
L'inégalité triangulaire donne: $AC+BC≥AB$
Soit: $2x – 5+x + 2≥7$
Soit: $3x-3≥7$
Soit: $x≥{10}/{3}$.
2.c. On suppose que le plus grand coté est AC.
L'inégalité triangulaire donne: $AB+BC≥AC$
Soit: $7+x + 2≥2x-5$
Soit: $7+2+5≥2x-x$
Soit: $14≥x$.
On suppose que le plus grand coté est BC.
L'inégalité triangulaire donne: $AB+AC≥BC$
Soit: $7+2x -5≥x+2$
Soit: $2x-x≥2-7+5$
Soit: $x≥0$.
2.d. Finalement, le triangle ABC existe si et seulement si
$x≥{10}/{3}$ et $14≥x$ et $x≥0$
Soit: ${10}/{3}≤x≤14$
Donc le triangle ABC existe si et seulement si $x$ est dans l'intervalle $[{10}/{3};14]$.