 Orthogonalité
Orthogonalité
Exercice 2
Un ballon décolle verticalement du point D.
Un observateur se situe au niveau du sol, au point O, situé à 2 km du point D.
Le ballon passe par le point $M_1$ puis par le point $M_2$.
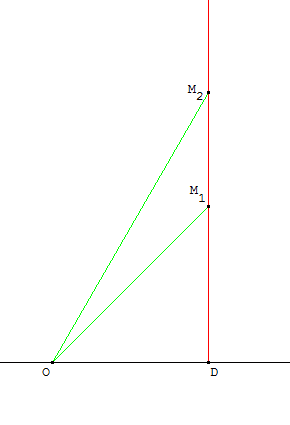
A l'aide d'un sextant, l'observateur mesure les angles ${DOM_1}↖{∧}$ et ${DOM_2}↖{∧}$.
Il trouve ${DOM_1}↖{∧}=45°$ et ${DOM_2}↖{∧}=60°$
1. Déterminer la distance $M_1M_2$.
2. Le ballon met 12 minutes et 12 secondes pour aller de $M_1$ à $M_2$.
Quelle est la vitesse moyenne du ballon entre $M_1$ et $M_2$?
On exprimera cette vitesse en m/s, puis en km/h.
3. On suppose que le ballon garde une vitesse constante tout au long de son ascension.
Une heure après son décollage, il se trouve en un point $M_3$.
Déterminer l'angle ${DOM_3}↖{∧}$ (arrondi au degré).
Corrigé
Les calculs de distances seront effectués avec des distances exprimées en km.
1. Le triangle $ODM_1$ est rectangle en D, et comme ${DOM_1}↖{∧}=45°$, ce triangle est isorectangle en O.
Donc: $DM_1=DO$.
Et par là: $DM_1=2$
Le triangle $ODM_2$ est rectangle en D, ce qui permet les calculs suivants.
Première méthode.
$\cos {DOM_2}↖{∧}={OD}/{OM_2}$.
Et donc: $OM_2={OD}/{\cos {DOM_2}↖{∧}}={2}/{\cos 60°}={2}/{{1}/{2}}=4$.
$DM_2^2=OM_2^2-OD_2^2=4^2-2^2=16-4=12$
Et par là: $DM_2=√{12}$
Seconde méthode.
$\tan {DOM_2}↖{∧}={DM_2}/{OD}$.
Et donc: $\tan {DOM_2}↖{∧} × OD=DM_2$
D'où: $DM_2= \tan 60° × 2=√{3}× 2=√{12}$
Et finalement: $M_1M_2=DM_2-DM_1=√{12}-2≈1,464$.
La distance $M_1M_2$ vaut environ 1,464 km, c'est à dire environ $1\,464$ m.
2. La distance $M_1M_2$ a été parcourue en 12 minutes et 12 secondes.
Or: $12×60+12=732$.
Donc les $1\,464$ mètres ont été parcourus en 732 secondes.
On calcule: ${1464}/{732}=2$.
La vitesse ascensionnelle moyenne du ballon entre $M_1$ et $M_2$ est d'environ 2 m/s.
On rappelle qu'une heure contient $3\,600$ secondes, et qu'un kilomètre représente $1\,000$ mètres.
On calcule donc: $2×{3\,600}/{1\,000}=7,2$.
La vitesse ascensionnelle moyenne du ballon entre $M_1$ et $M_2$ est d'environ 7,2 km/h.
On aurait pu également expliquer que 2 m/s représentent $2×{3\,600}=7\,200$ m/h,
et donc ${7\,200}/{1\,000}=7,2$ km/h
3. La distance $DM_3$ a été parcourue en 3600 secondes à une vitesse de 2 m/s.
On calcule: $2×3\,600=7\,200$.
Et comme 7200 mètres représentent 7,2 km, on a: $DM_3=7,2$.
Le triangle $ODM_3$ est rectangle en D, ce qui permet les calculs suivants.
$\tan {DOM_3}↖{∧}={DM_3}/{OD}={7,2}/{2}=3,6$.
Et par là: ${DOM_3}↖{∧}≈74°$ (obtenu à l'aide de la calculatrice à l'aide de la "touche" Arctan)