 Orthogonalité
Orthogonalité
Exercice 4
Partie A
Soit ABC un triangle n'ayant que des angles aigus. Soit H le projeté orthogonal de A sur [BC].
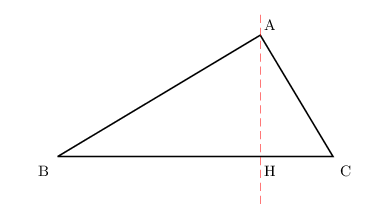
- Montrer que l'aire $s$ de ABC vérifie les égalités: $s={BC×AC×\sin {C}↖{∧} }/{2}={BC×AB×\sin {B}↖{∧} }/{2}$
- On pose $a=BC$, $b=CA$ et $c=AB$.
Montrer que ${a}/{\sin {A}↖{\^}}={b}/{\sin {B}↖{\^}}={c}/{\sin {C}↖{\^}}$
Ces égalités s'appellent la loi des sinus.
On admettra qu'elles sont vraies pour n'importe quel triangle ABC (non aplati). Cela suppose que les sinus des angles obtus existent; vous en verrez la définition en première.
Partie B
Soit ABC un triangle tel que $AB=400$, ${A}↖{∧}=40°$ et ${B}↖{∧}=60°$.
Soit (BN) une droite passant par B selon le dessin suivant.
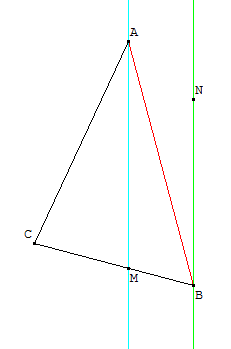
On suppose que ${NBA}↖{∧}=15°$
Le point M est alors sur [BC], et (AM) et (BN) sont parallèles.
- Déterminer une mesure de ${MAB}↖{∧}$.
- Déterminer une mesure de ${BMA}↖{∧}$.
- A l'aide de la loi des sinus, déterminer les distances AM, MB et CB (arrondies à 0,01 près).
Partie C
On reprend le graphique de la partie B, et on y ajoute le point E.
On suppose que ${CBE}↖{∧}=50°$ et ${ECB}↖{∧}=80°$
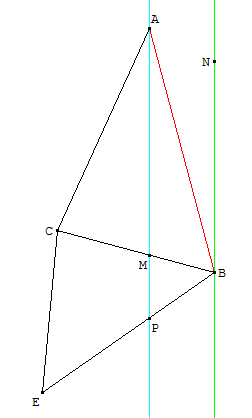
Le point P est à l'intersection de la droite (AM) et du segment [BE].
- Déterminer une mesure de ${BEC}↖{∧}$.
- A l'aide de la loi des sinus, déterminer la distance EB (arrondie à 0,01 près).
- Déterminer une mesure de ${BPM}↖{∧}$.
- A l'aide de la loi des sinus, déterminer la distance MP (arrondie à 0,01 près).
Corrigé
Partie A
-

H est le projeté orthogonal de A sur [BC].
Donc $\sin {C}↖{∧} ={AH}/{AC}$ (dans le triangle AHC rectangle en H)
Et par là: $AH=AC×\sin {C}↖{∧}$
Par aileurs, comme H est le projeté orthogonal de A sur [BC], ABC a pour aire: $s={BC×AH }/{2}$.
Donc finalement, on obtient: $s={BC×AC×\sin {C}↖{∧} }/{2}$
Les rôles joués par B et C sont similaires. Donc, si on les permute dans les lignes qui précèdent, le raisonnement reste vrai.
Et on obtient: $s={BC×AB×\sin {B}↖{∧} }/{2}$
Donc l'aire $s$ de ABC vérifie les égalités: $s={BC×AC×\sin {C}↖{∧} }/{2}={BC×AB×\sin {B}↖{∧} }/{2}$ - On pose $a=BC$, $b=CA$ et $c=AB$.
Les deux membres de droite de l'égalité précédente donnent: ${ a×b×\sin {C}↖{∧} }/{2}={a×c×\sin {B}↖{∧} }/{2}$
Et donc, en multipliant par ${2}/{a}$, on obtient: $b×\sin {C}↖{∧}=c×\sin {B}↖{∧}$
Et par là: ${b}/{\sin {B}↖{\^}}={c}/{\sin {C}↖{\^}}$
Et, comme A, B et C jouent des rôles semblables, on obtient finalement:
${a}/{\sin {A}↖{\^}}={b}/{\sin {B}↖{\^}}={c}/{\sin {C}↖{\^}}$
Partie B

- Comme (AM) et (BN) sont parallèles, les angles alternes internes ${NBA}↖{∧}$ et ${MAB}↖{∧}$ ont même mesure, et donc ${MAB}↖{∧}={NBA}↖{∧}$
Soit: ${MAB}↖{∧}=15°$ - Dans le triangle ABM, on a: ${MAB}↖{∧}+{ABM}↖{∧}+{BMA}↖{∧}=180°$.
Soit: $15°+60°+{BMA}↖{∧}=180°$.
Et donc: ${BMA}↖{∧}=105°$ - On applique la loi des sinus dans ABM.
${MB}/{\sin {MAB}↖{∧}}={AM}/{\sin {ABM}↖{∧}}={AB}/{\sin {BMA}↖{∧}}$
Soit: ${MB}/{\sin 15°}={AM}/{\sin 60°}={400}/{\sin 105°}$
Et donc: $MB={400}/{\sin 105°}×\sin 15°≈$$107,18$
On remarquera que la calculatrice est capable de calculer le sinus de $105°$ bien que cet angle soit un angle obtus.
Et: $AM={400}/{\sin 105°}×\sin 60°≈$ $358,63$
Pour trouver CB, on applique la loi des sinus dans le triangle ABC.
Tout d'abord, comme ${A}↖{∧}=40°$ et ${B}↖{∧}=60°$, on a ${C}↖{∧}=80°$
Or, la loi des sinus donne: ${CB}/{\sin {CAB}↖{∧}}={AC}/{\sin {ABC}↖{∧}}={AB}/{\sin {BCA}↖{∧}}$
Donc: ${CB}/{\sin 40°}={AC}/{\sin 60°}={400}/{\sin 80°}$
Et par là: $CB={400}/{\sin 80°}×\sin 40°≈$$261,08$
Partie C

- Dans le triangle CBE, on a: ${BEC}↖{∧}+{EBC}↖{∧}+{BCE}↖{∧}=180°$.
Soit: ${BEC}↖{∧}+50°+80°=180°$.
Et donc: ${BEC}↖{∧}=50°$ - On applique la loi des sinus dans CEB. ${CB}/{\sin {BEC}↖{∧}}={EB}/{\sin {ECB}↖{∧}}$
Donc: ${261,08}/{\sin {50°}↖{∧}}≈{EB}/{\sin 80°}$
Et donc: $EB≈{261,08}/{\sin 50°}×\sin 80°≈$$335,64$
- Comme (MP) et (BN) sont parallèles, on obtient: ${BPM}↖{∧}=180°-{PBN}↖{∧}$
Or: ${PBN}↖{∧}={PBM}↖{∧}+{MBA}↖{∧}+{ABN}↖{∧}=50°+60°+15°=125°$
Donc: ${BPM}↖{∧}=180°-125°$
Soit: ${BPM}↖{∧}=55°$ - On applique la loi des sinus dans MPB. ${MP}/{\sin {MBP}↖{∧}}={BM}/{\sin {BPM}↖{∧}}$
Donc: ${MP}/{\sin 50°}≈{107,18}/{\sin 55°}$
Et donc: $MP≈{107,18}/{\sin 55°}×\sin 50°≈$$100,23$
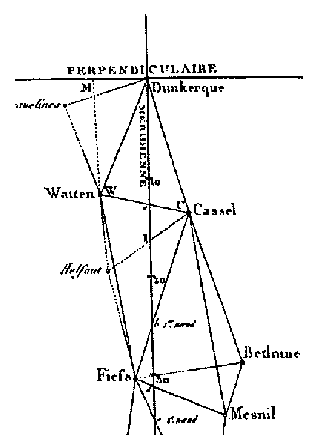
Les calculs précédents sont des calculs de triangulation. Répétés de très nombreuses fois, ils ont permis à
Delambre et Méchain, entre 1791 et 1798, de calculer la longueur de l’arc de méridien reliant Dunkerque à Barcelone afin de définir le mètre comme étant le dix millionième du quart du méridien terrestre.
En effet, à l'époque, l'unité de longueur en France était la toise (environ 1,949 m), et la Révolution Française voulait imposer un système métrique basé sur des considérations universelles. L'arc de méridien répondait à ces exigences car il n'appartient à aucune nation.
Pour information, la droite (BN) pointait vers le Nord. Les segments [AM] et [MP] étaient des morceaux de méridien. Et la somme de toutes les distances de ce type a donné la longueur totale de l'arc de méridien.
La difficulté initiale était de mesurer une base AB avec précision, chose faite grace à 4 règles de platine de 2 toises chacune, la distance AB initiale étant d'environ 11 km. La mesure des angles était effectuée en utilisant un cercle répétiteur.
On notera que le modèle utilisé dans cet exercice est simplifié. Les calculs étaient en réalité plus complexes à cause des différences d'altitude entre les points.
Ci-dessous un extrait des mesures réelles.
L'exercice 7 sur le produit scalaire du cours de première propose des calculs de triangulation qui prennent en compte les différences de hauteur entre les points d'observation.