Pourcentages
Pourcentages
Exercice 3
- Le 1er janvier de l'année, Jean place 1000 euros au taux annuel de 3%.
Chaque fin d'année, il ajoute 100 euros sur ce compte.
Expliquer pourquoi le capital disponible au début de la seconde année est de 1130 euros. - Expliquer pourquoi le capital disponible au début de la troisième année est de 1263,90 euros.
- Compléter l'algorithme suivant pour qu'à la fin de son exécution, la variable U contienne le capital disponible au début de la onzième année.
$U$ ← 1000
Pour $I$ allant de 1 à ...
$U$ ← ...
Fin du Pour
- Ecrire en Python un programme correspondant à l'algorithme précédent. A la fin de son exécution, le programme affichera le capital disponible au début de la onzième année.
- Proposer un algorithme tel que, à la fin de son exécution, la variable N contienne le nombre d'années nécessaires pour que le capital disponible vaille au moins 2000 euros.
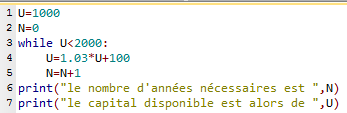
- Ecrire en Python un programme correspondant à l'algorithme précédent. A la fin de son exécution, le programme affichera la valeur de N et le capital disponible.
Corrigé
- A la fin de la première année, le capital disponible vaut: $1000×1,03=1030$ euros.
Au début de la seconde année, il vaut donc: $1030+100=1130$ euros. - A la fin de la seconde année, le capital disponible vaut: $1130×1,03=1163,90$ euros.
Au début de la troisième année, il vaut donc: $1163,90+100=1263,90$ euros. - Ici, nous devons faire 10 boucles. On utilise un Pour.
Algorithme complété:
$U$ ← 1000
Pour $I$ allant de 1 à 10
$U$ ← $1,03×U+100$
Fin du Pour
Noter le 10, et non pas un 11, dans la seconde ligne (sinon, il y aurait une boucle de trop) - Voici un programme convenable

- Un algorithme possible:
$U$ ← 1000
$N$ ← 0
Tant que $U<2000$
$U$ ← $1,03×U+100$
$N$ ← $N+1$
Fin du Pour
Ici, on a utilisé un Tant que, et non pas un Pour, car le nombre de boucles est inconnu. - Voici un programme convenable