Probabilités
Exercice 3
Dans une usine, un technicien dispose d'un lot de 5 composants.
Trois sont de type A, deux sont de type B.
Les types sont très difficiles à identifier.
Le technicien prend au hasard un premier composant, puis un second, et il les monte dans un appareil
Mais l'appareil ne fonctionne que si les 2 composants sont de même type.
Soit A: "le composant est de type A".
Soit B: "le composant est de type B".
- Dresser un arbre de dénombrement décrivant l'expérience
- Déterminer la probabilité que l'appareil fonctionne.
Pour cette question, on supposera que l'appareil fonctionne.
On en sort un composant. Déterminer la probabilité que le composant soit de type A.
Corrigé
- Nous dressons un arbre de dénombrement décrivant l'expérience:
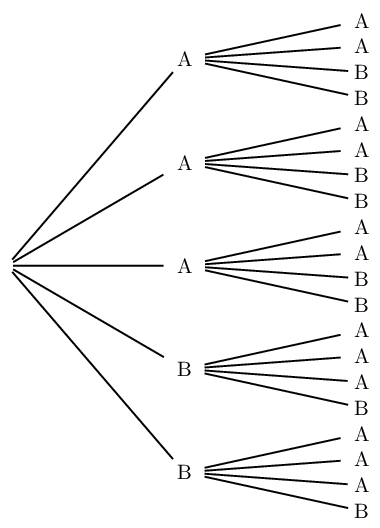
- Le nombre total d'issues est $5×4=20$.
Ces issues sont équiprobables.
8 issues sont favorables; ce sont les 6 cas où les composants de type A sont choisis et les 2 cas où les composants de type B sont choisis.
Donc la probabilité cherchée vaut: ${8}/{20}=0,4$.
La probabilité que l'appareil fonctionne vaut $0,4$. - On sait que l'appareil fonctionne. Donc l'univers se réduit aux 8 cas cités dans la question précédente.
Ces cas sont équiprobables.
6 cas sont favorables; ce sont les 6 cas où les composants de type A sont choisis.
Donc la probabilité cherchée vaut: ${6}/{8}=0,75$.
La probabilité que le composant soit de type A vaut $0,75$.