Les autres fonctions de référence
Exercice 1
- Résoudre l'équation (1): ${1}/{x}=0,5$.
- Résoudre l'équation (2): ${5}/{x}-9=0$.
- Résoudre l'inéquation (3): ${1}/{x}≤0,5$.
- Résoudre l'inéquation (4): ${1}/{x}≥0,2$.
- Résoudre l'inéquation (5): $3+{1}/{x}≥0$.
- Résoudre l'équation (6): ${1}/{3x-10}=0,5$.
- Résoudre l'équation (7): ${6}/{x-2}-3,5=0$.
Résoudre l'inéquation (8): ${1}/{x-2}≤0,5$.- Résoudre l'inéquation (9):${6}/{x-2}-3,5$<$0$.
- Résoudre l'inéquation (10): ${1}/{x}-{1}/{x-1}≤0$.
Solution...
Corrigé
A retenir: dans une équation ou une inéquation dont le membre de droite est nul,
si le membre de gauche contient des $x$ uniquement sous la forme ${k}/{g(x)}$,
alors il est conseillé d'isoler ce quotient.
- Nous sommes en présence d'un quotient. Il peut y avoir des valeurs interdites!
Ici, la seule valeur interdite est $0$.
Le domaine d'étude est: $\D_E=\ℝ ∖\{0\}$
Résolution:
(1) $⇔$ ${1}/{x}=0,5$ $⇔$ $x={1}/{0,5}=2$
S$=\{2\}$
A retenir: si $a≠0$, alors: ${1}/{x}=a$ $⇔$ $x={1}/{a}$. - Nous sommes en présence d'un quotient. Il peut y avoir des valeurs interdites!
On a évidemment: $\D_E=\ℝ ∖\{0\}$
(2) $⇔$ ${5}/{x}-9=0$ $⇔$ ${5}/{x}=9$ $⇔$ ${1}/{x}={9}/{5}$ $⇔$ $x={5}/{9}$
S$=\{{5}/{9}\}$ - On a évidemment: $\D_E=\ℝ ∖\{0\}$
Résolution:
(3) $⇔$ ${1}/{x}≤0,5$
Pour résoudre une telle inéquation, il faut avoir en tête l'allure de l'hyperbole représentant la fonction inverse
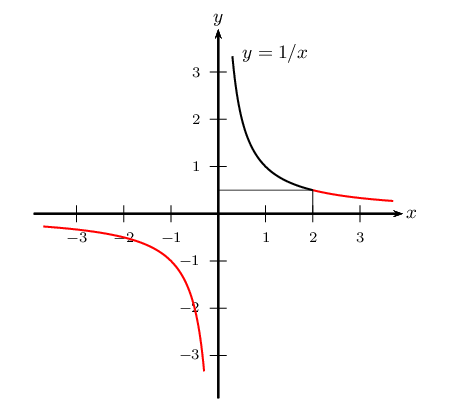
On remarque que ${1}/{x}=0,5$ $⇔$ $x=2$.
On obtient: (3) $⇔$ $x$<$0$ ou $x≥{1}/{0,5}$
Soit: (3) $⇔$ $x$<$0$ ou $x≥2$
S$=]- ∞; 0[ ⋃ [2;+∞[$ - On a évidemment: $\D_E=\ℝ ∖\{0\}$
Résolution:
(4) $⇔$ ${1}/{x}≥0,2$
Pour résoudre une telle inéquation, il faut avoir en tête l'allure de l'hyperbole représentant la fonction inverse
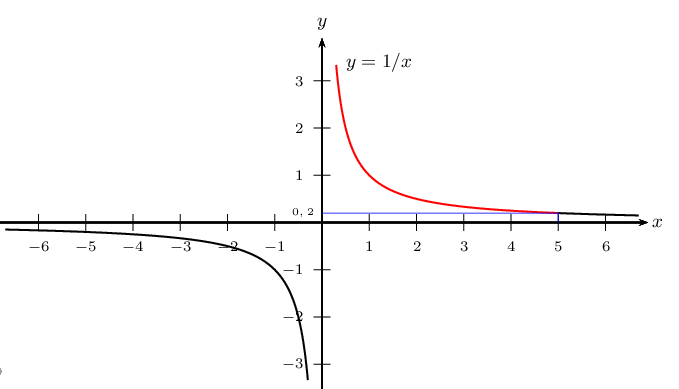
On remarque que ${1}/{x}=0,2$ $⇔$ $x={1}/{0,2}=5$.
On obtient: (4) $⇔$ $0$<$x≤5$
S$=]0:5]$ - On a évidemment $\D_E=\ℝ ∖\{0\}$
On isole l'inverse. On a : (5) $⇔$ ${1}/{x}≥-3$
Pour résoudre une telle inéquation, il faut avoir en tête l'allure de l'hyperbole représentant la fonction inverse
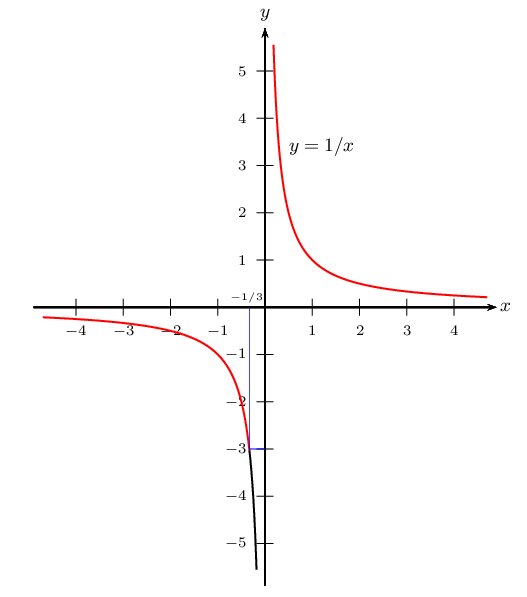
On obtient: (5) $⇔$ $x≤{1}/{-3}$ ou $x$>$0$
S$=]- ∞; -{1}/{3}] ⋃ ]0;+∞[$ -
On doit avoir $3x-10≠0$, et donc: $x≠{10}/{3}$.
Donc le domaine d'étude est: $\D_E=\ℝ ∖\{{10}/{3}\}$
Résolution:
On a là un quotient du type ${1}/{g(x)}$, ce qui permet de procéder comme au 1.
(6) $⇔$ ${1}/{3x-10}=0,5$ $⇔$ $3x-10={1}/{0,5}$ $⇔$ $3x=2+10$
Soit: (6) $⇔$ $x={12}/{3}=4$
S$=\{4\}$
- On doit avoir $x-2≠0$, et donc: $x≠2$.
Donc: $\D_E=\ℝ ∖\{2\}$
On va isoler un quotient du type ${1}/{g(x)}$ pour procéder comme au 6.
(7) $⇔$ ${6}/{x-2}-3,5=0$ $⇔$ ${6}/{x-2}=3,5$
Soit: (7) $⇔$ ${1}/{x-2}={3,5}/{6}$
Soit: (7) $⇔$ $x-2= {6}/{3,5}$
Soit: (7) $⇔$ $x= 2+{6}/{3,5}={14}/{7}+{12}/{7}={26}/{7}$
S$=\{{26}/{7}\}$ - Comme dans l'équation (7), on a: $\D_E=\ℝ ∖\{2\}$
On va isoler un quotient du type ${1}/{g(x)}$ pour procéder comme au 3.
On obtient donc: (8) $⇔$ ${1}/{x-2}≤0,5$
Or, on a vu précédemment que: ${1}/{x-2}=0,5$ $⇔$ $x-2= 2$
Et connaissant l'allure de l'hyperbole représentant la fonction inverse, on obtient:
(8) $⇔$ $x-2$<$0$ ou $x-2≥2$
Soit: (8) $⇔$ $x$<$2$ ou $x≥2+2$
Soit: (8) $⇔$ $x$<$2$ ou $x≥4$
S$=]- ∞; 2[ ⋃ [4;+∞[$
- Comme dans l'équation (7), on a: $\D_E=\ℝ ∖\{2\}$
On va isoler un quotient du type ${1}/{g(x)}$ pour procéder comme au 3.
On obtient donc: (9) $⇔$ ${6}/{x-2}$<$3,5$ $⇔$ ${1}/{x-2}$<${3,5}/{6}$
La division par 6 n'a pas changé le sens de l'inégalité car 6 est strictement positif
Or, on a vu précédemment que: ${1}/{x-2}={3,5}/{6}$ $⇔$ $x-2= {6}/{3,5}$
Et connaissant l'allure de l'hyperbole représentant la fonction inverse, on obtient:
(9) $⇔$ $x-2$<$0$ ou $x-2$>${6}/{3,5}$
Soit: (9) $⇔$ $x$<$2$ ou $x$>$2+{6}/{3,5}$
Soit: (9) $⇔$ $x$<$2$ ou $x$>${26}/{7}$
S$=]- ∞; 2[ ⋃ ]{26}/{7};+∞[$
- On doit avoir $x≠0$ et $x-1≠0$, et donc: $x≠0$ et $x≠1$.
Donc: $\D_E=\ℝ ∖\{0;1\}$
(10) $⇔$ ${1}/{x}-{1}/{x-1}≤0$
Il est impossible d'isoler tous les $x$ dans un unique quotient du type ${k}/{g(x)}$. Par contre, on peut réduire au même dénominateur.
(10) $⇔$ ${x-1}/{x(x-1)}-{x}/{x(x-1)}≤0$
(10) $⇔$ ${x-1-x}/{x(x-1)}≤0$
(10) $⇔$ ${-1}/{x(x-1)}≤0$
Nous allons chercher le signe du membre de gauche; nous repèrerons en particulier les valeurs de $x$ pour lesquelles ce membre est négatif.
Nous sommes en présence d'un quotient. Son numérateur $-1$ est strictement négatif. Son dénominateur est le produit de $x$ par $x-1$.
La fonction $x$ est linéaire et son signe est évident.
La fonction $x-1$ est affine; elle s'annule pour $x=1$, et son coefficient directeur est strictement positif (il vaut 1).
D'où le tableau de signes suivant:
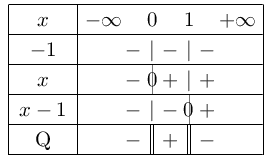
On cherche pour quels $x$ le quotient est négatif.
On obtient donc: $x$<$0$ ou $x$>$1$.
Donc: S$=]- ∞; 0[ ⋃ ]1;+∞[$