Corrigé

A retenir: dans une équation ou une inéquation dont le membre de droite est nul,
si le membre de gauche contient des $x$ uniquement sous la forme $√{g(x)}$,
alors il est conseillé d'isoler cette racine carrée.

1. Nous sommes en présence d'une racine. Il peut y avoir des valeurs interdites!
   Ici, les seules valeurs interdites sont les réels strictement négatifs.
   Le domaine d'étude est: $\D_E=[0;+∞[$
   
   Résolution:
   (1) $⇔$ $√{x}=3$ $⇔$ $x=3^2=9$
   S$=\{9\}$
   A retenir: si $a≥0$, alors: $√{x}=a$ $⇔$ $x=a^2$.


2. Nous sommes en présence d'une racine. Il peut y avoir des valeurs interdites!
   On a évidemment: $\D_E=[0;+∞[$
   
   (2) $⇔$ $2√{x}-9=0$ $⇔$ $2√{x}=9$ $⇔$ $√{x}={9}/{2}=4,5$ $⇔$ $x=4,5^2=20,25$
   S$=\{20,25\}$


3. On a évidemment: $\D_E=[0;+∞[$
   
   Résolution:
   (3) $⇔$ $√{x}≤4$
   Pour résoudre une telle inéquation, il faut avoir en tête l'allure de la demi-parabole représentant la fonction racine carrée
   
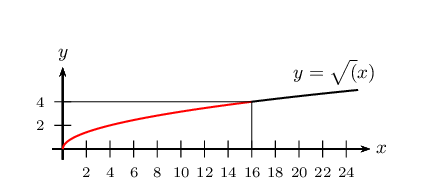
   On remarque que $√{x}=4$ $⇔$ $x=4^2=16$.
   On obtient: (3) $⇔$ $0≤x≤16$
   S$=[0;16]$
   


4. On a évidemment: $\D_E=[0;+∞[$
   
   Résolution:
   (4) $⇔$ $√{x}≥1,5$
   Pour résoudre une telle inéquation, il faut avoir en tête l'allure de la demi-parabole représentant la fonction racine carrée
   
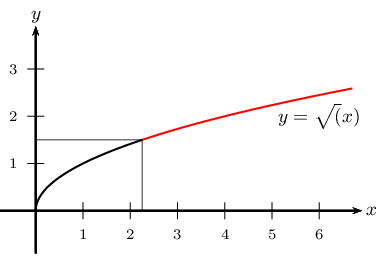
   On remarque que $√{x}=1,5$ $⇔$ $x=1,5^2=2,25$.
   On obtient: (4) $⇔$ $2,25≤x$
   S$=[2,25;+∞[$
   


5. On doit avoir $x-2≥0$, et donc: $x≥2$.
   Donc: $\D_E=[2;+∞[$
   
   (5)$⇔$ $√{x-2}=3$ $⇔$ $x-2=3^2=9$
   Soit: (5)$⇔$ $x=9+2$
   Soit: (5)$⇔$ $x=11$
   S$=\{11\}$