Statistiques
Exercice 2
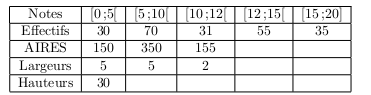
Les moyennes en mathématique des élèves du lycée Glandouille sont résumées dans le tableau suivant :
On suppose que les répartitions des notes sont "régulières" à l'intérieur de chaque classe.
Dans cet exercice, sauf indication contraire, les calculs seront détaillés, et les résultats seront arrondis
si besoin à 0,001 près.
1. a. Déterminer les fréquences associées à chacune des classes du tableau.
On rappelle que la fréquence cumulée croissante associée à une classe correspond à la somme de la fréquence de la classe et des fréquences des classes inférieures.
Déterminer les fréquences cumulées croissantes associées à chacune des classes du tableau.
1. b. Quel pourcentage des élèves a une moyenne supérieure à 10 ?
2. On rappelle que polygone des fréquences cumulées croissantes d'une série associe à chaque extrémité supérieure d'une classe sa fréquence cumulée croissante.
Faire une figure représentant le polygone des fréquences cumulées croissantes de la série.
3. Soit $f_8$ le pourcentage d'élèves ayant une moyenne inférieure à 8.
Déterminer graphiquement un encadrement d'amplitude $1%$ de $f_8$.
Soit $n$ le nombre d'élèves que cela représente. Donner un encadrement de $n$ d'amplitude 3.
4. Déterminer graphiquement la médiane $m$ de la série (arrondie à 0,1 près).
Que signifie cette valeur ?
5. Nous allons représenter cette série par un histogramme, dans lequel l'aire de chaque rectangle sera proportionnelle à l'effectif associé.
Recopier et compléter le tableau suivant, donnant les hauteurs (arrondies éventuellement à 0,1
près) des rectangles de l'histogramme.
Puis construire l'histogramme de la série.
6. Déterminer la moyenne $\ov x$ de la série.
Solution...
Corrigé
1.a. Les fréquences et les fréquences cumulées croissantes associées à chacune des classes sont dans le tableau
ci-dessous.
Par exemple :
on a calculé ${70}/{221}≈0,317$ pour obtenir la fréquence de $31,7 %$;
on a calculé $13,6 +31,7 +14= 59,3 $ pour obtenir la fréquence cumulée de $59,3 %$.
1. b. On constate que le pourcentage d'élèves ayant une moyenne strictement inférieure à 10 est d'environ $45,3%$.
Donc $54,7%$ des élèves a une moyenne supérieure à 10.
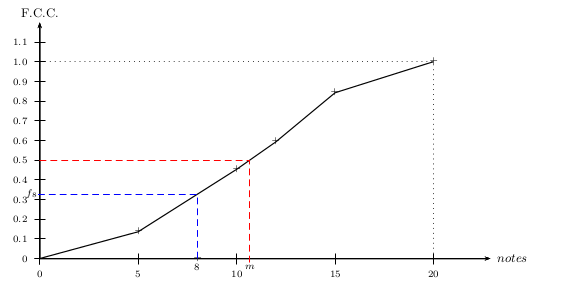
2. Le polygone des fréquences cumulées croissantes de la série est donné ci-dessous.
A retenir.
Ne pas associer les F.C.C. aux centres des classes !
Par exemple, la F.C.C. de $100%$ correspond au nombre 20 (extrémité supérieure de la dernière classe) (et pas au nombre 17,5).
En effet, $100%$ des élèves ont une moyenne inférieure ou égale à 20 (mais pas à 17,5)...
3. Graphiquement, on constate que : $32%$<$f_8$<$33%$.
Or, on a : ${n}/{221}=f_8 $, et par là : $n=f_8 ×221$.
Pour $f_8=0,32$, on obtient : $f_8 ×221=70,72$
Pour $f_8=0,33$, on obtient : $f_8 ×221=72,93$
Par conséquent : $70$<$n$<$73$.
4. Graphiquement la médiane $m$ de la série est d'environ 10,7.
Environ $50%$ des élèves ont une note moyenne inférieure à 10,7.
5. Le tableau proposé est complété ci-dessous.
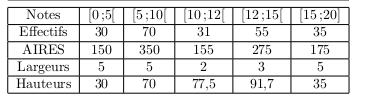
L'aire de chaque rectangle est proportionnelle à l'effectif associé. Ici, le coefficient vaut 5.
Considérons par exemple la colonne de la classe [12;15[.
Comme chaque aire est égale à 5 fois l'effectif associé, on obtient : $55×5=275$.
La largeur du rectangle est : $15-12=3$.
La hauteur du rectangle est : ${275}/{3}≈91,7$.
L'histogramme est tracé ci-dessous.
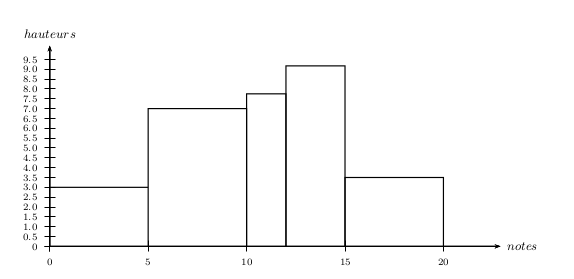
A retenir :
Dans un histogramme correct, les aires des rectangles sont proportionnelles aux effectifs.
Mais les hauteurs des rectangles ne sont pas proportionnelles aux effectifs, sauf si toutes les classes ont la même largeur !
Attention ! LES HISTOGRAMMES PRODUITS PAR CERTAINS TABLEURS NE RESPECTENT PAS CETTE PROPRIETE !
6. $\ov x={2,5×30+7,5×70+11×31+13,5×55+17,5×35}/{221}≈10,389$.
La moyenne de la série est d'environ 10,389.
A retenir : Dans ce calcul, chaque classe est remplacée par son milieu. Cela se conçoit car la répartition des notes est supposée régulière dans chaque classe.