 Les vecteurs
Les vecteurs
Exercice 1
Les 3 parties sont indépendantes.
Partie A
On considère la figure ci-dessous, pour laquelle:
ABCD est un parallélogramme
$t_{{BC}↖{→}}(D)=E$
${AB}↖{→}={EF}↖{→}$
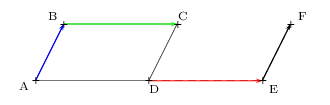
1.
Sans justifier,compléter les affirmations suivantes:
${AB}↖{→}={D.}↖{→}$
${BC}↖{→}={A.}↖{→}$
${CF}↖{→}={.D}↖{→}$
${BD}↖{→}={C.}↖{→}$
$t_{{BA}↖{→}}(C)=.$
$t_{{A.}↖{→}}(C)=F$
$t_{{ED}↖{→}}(.)=B$
2. Les conjectures du 1. ne sont que des hypothèses.
De même, il semble que DCFE est un parallélogramme.
Prouver le.
Partie B
On considère 4 points A, B, C et E.
Le point D est défini par l'égalité vectorielle: ${AD}↖{→}={AB}↖{→}+{AC}↖{→}$
Le point F est défini par l'égalité vectorielle: ${EF}↖{→}={CD}↖{→}$
1. Faire une figure.
2. Montrer que ${EF}↖{→}={AB}↖{→}$
3. Quelle est l'image du point B par la translation de vecteur ${AE}↖{→}$?
Partie C
On considère la figure ci-dessous, pour laquelle:
ABCD est un parallélogramme
$t_{{BC}↖{→}}(D)=E$
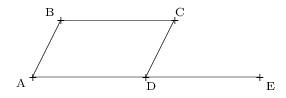
1.
Sans justifier,compléter les affirmations suivantes:
a. ${AD}↖{→}+{DC}↖{→}={A.}↖{→}$
b. ${BC}↖{→}+{BA}↖{→}={B.}↖{→}$
c. ${BC}↖{→}+{C.}↖{→}={BE}↖{→}$
d. ${AD}↖{→}-{BA}↖{→}={.C}↖{→}$
e. $2{BC}↖{→}={.E}↖{→}$
2. Les conjectures du 1. ne sont que des hypothèses.
Démontrer les égalités du 1.
Corrigé
Partie A
1.
On obtient:
${AB}↖{→}={DC}↖{→}$
${BC}↖{→}={AD}↖{→}$
${CF}↖{→}={AD}↖{→}$
${BD}↖{→}={CE}↖{→}$
$t_{{BA}↖{→}}(C)=D$
$t_{{AD}↖{→}}(C)=F$
$t_{{ED}↖{→}}(C)=B$

2. Pour montrer que DCFE est un parallélogramme, il suffit de prouver une égalité entre 2 vecteurs convenables.
ABCD est un parallélogramme. Donc: ${AB}↖{→}={DC}↖{→}$
Or, on a: ${AB}↖{→}={EF}↖{→}$.
Donc: ${DC}↖{→}={EF}↖{→}$
Et par là, DCFE est un parallélogramme.
Partie B
A savoir pour faire cette partie de l'exercice.
La propriété fondamentale concernant les vecteurs:
${AB}↖{→}={DC}↖{→}$ si et seulement si ABCD est un parallélogramme.
La règle du parallélogramme:
${OA}↖{→}+{OB}↖{→}={OM}↖{→}$ si et seulement si OAMB est un parallélogramme.
Cette règle fait intervenir 4 points.
A ne pas confondre avec:
La relation de Chasles: ${AM}↖{→}+{MB}↖{→}={AB}↖{→}$.
Cette relation fait intervenir 3 points.
Elle n'est pas utilisée dans cette partie B.
1. Une figure convenable est proposée ci-dessous.
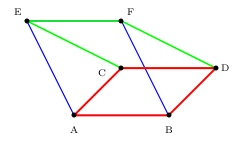
2. On sait que: ${AD}↖{→}={AB}↖{→}+{AC}↖{→}$ (par hypothèse).
Donc ABDC est un parallélogramme.
Et par là: ${AB}↖{→}={CD}↖{→}$.
Or: ${EF}↖{→}={CD}↖{→}$ (par hypothèse).
On en déduit donc que: ${EF}↖{→}={AB}↖{→}$.
3. Comme ${EF}↖{→}={AB}↖{→}$, on en déduit que EFBA est un paralléogramme.
Par conséquent, l'image du point B par la translation de vecteur ${AE}↖{→}$ est le point F.
Partie C
On considère la figure ci-dessous, pour laquelle:
ABCD est un parallélogramme
$t_{{BC}↖{→}}(D)=E$

1.
On obtient:
a. ${AD}↖{→}+{DC}↖{→}={AC}↖{→}$
b. ${BC}↖{→}+{BA}↖{→}={BD}↖{→}$
c. ${BC}↖{→}+{CE}↖{→}={BE}↖{→}$
d. ${AD}↖{→}-{BA}↖{→}={AC}↖{→}$
e. $2{BC}↖{→}={AE}↖{→}$
2. a. D'après la relation de Chasles, on a: ${AD}↖{→}+{DC}↖{→}={AC}↖{→}$
b. Comme ABCD est un parallélogramme, on a: ${BC}↖{→}+{BA}↖{→}={BD}↖{→}$
c. D'après la relation de Chasles, on a: ${BC}↖{→}+{CE}↖{→}={BE}↖{→}$
d. On a: ${AD}↖{→}-{BA}↖{→}={AD}↖{→}+{AB}↖{→}$
Et, comme ABCD est un parallélogramme, on obtient alors: ${AD}↖{→}-{BA}↖{→}={AC}↖{→}$
e. On a: $2{BC}↖{→}={BC}↖{→}+{BC}↖{→}$
Or, comme ABCD est un parallélogramme, on sait que: ${BC}↖{→}={AD}↖{→}$
Et, comme $t_{{BC}↖{→}}(D)=E$, on sait que: ${BC}↖{→}={DE}↖{→}$
Par conséquent, on obtient: $2{BC}↖{→}={AD}↖{→}+{DE}↖{→}$
Soit: $2{BC}↖{→}={AE}↖{→}$ (d'après la relation de Chasles)