Les vecteurs
Exercice 3
ABC est un triangle tel que I soit le milieu du côté [AB].
Le point K est défini par l'égalité vectorielle: ${IK}↖{→}=0,5{BC}↖{→}$
1. Faire une figure.
2. Exprimer ${AI}↖{→}$ en fonction de ${AB}↖{→}$.
3. 
En utilisant deux fois la relation de Chasles, démontrer que ${AK}↖{→}=0,5{AC}↖{→}$.
4. Qu'en déduire concernant le point K?
Solution...
Corrigé
1. Une figure convenable est tracée ci-dessous.
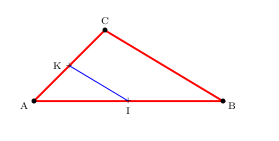
2. Le point I est le milieu du côté [AB], donc: ${AI}↖{→}=0,5{AB}↖{→}$.
3. A retenir: pour exprimer le vecteur ${AK}↖{→}$ en fonction du vecteur ${AC}↖{→}$, il suffit de décomposer ${AK}↖{→}$ à l'aide de la relation de Chasles.
L'astuce est de "suivre" les traits de construction, ce qui sous-tend l'utilisation des hypothèses données dans l'énoncé.
On a: ${AK}↖{→}={AI}↖{→}+{IK}↖{→}$ (d'après la relation de Chasles)
Soit: ${AK}↖{→}=0,5{AB}↖{→}+0,5{BC}↖{→}$ (d'après le 2., et par hypothèse)
Donc: ${AK}↖{→}=0,5({AB}↖{→}+{BC}↖{→})$
Donc: ${AK}↖{→}=0,5{AC}↖{→}$ (d'après la relation de Chasles)
4. On vient de montrer que ${AK}↖{→}=0,5{AC}↖{→}$.
Par conséquent, le point K est le milieu du segment [AC].