 Les vecteurs
Les vecteurs
Exercice 5
On considère le plan muni du repère orthonormé $(A,B,C)$.
Le point K est défini par l'égalité vectorielle: ${AK}↖{→}=3{AB}↖{→}$
Le point L est défini par l'égalité vectorielle: ${CL}↖{→}=2{AC}↖{→}$
1. Faire une figure.
2.a. Déterminer les coordonnées de K.
2.b. Montrer que ${AL}↖{→}=3{AC}↖{→}$, puis déterminer les coordonnées de L.
3. Déterminer les coordonnées des vecteurs ${LK}↖{→}$ et ${CB}↖{→}$.
4. Qu'en déduire concernant les droites (LK) et (CB)?
Solution...
Corrigé
1. Une figure convenable est tracée ci-dessous.
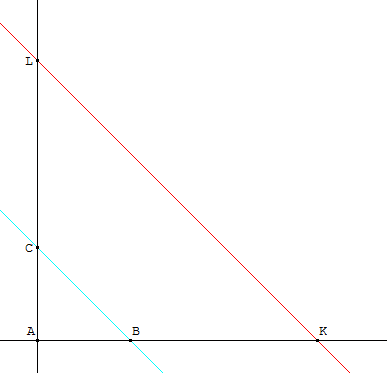
2.a. On a: ${AK}↖{→}=3{AB}↖{→}$
Donc: ${AK}↖{→}=3{AB}↖{→}+0{AC}↖{→}$
Donc K a pour coordonnées (3;0)
2.b. On a: ${CL}↖{→}=2{AC}↖{→}$
Donc: ${AC}↖{→}+{CL}↖{→}={AC}↖{→}+2{AC}↖{→}$
Soit: ${AL}↖{→}=3{AC}↖{→}$ (on a: ${AC}↖{→}+{CL}↖{→}={AL}↖{→}$ d'après la relation de Chasles)
Et donc: ${AL}↖{→}=0{AB}↖{→}+3{AC}↖{→}$
Donc L a pour coordonnées (0;3)
Le passage de ${CL}↖{→}=2{AC}↖{→}$ à ${AL}↖{→}=3{AC}↖{→}$ est tellement évident qu'on ne le détaille pas en général.
3. On a: $x_{{LK}↖{→}}=x_K-x_L=3-0=3$
Et on a: $y_{{LK}↖{→}}=y_K-y_L=0-3=-3$
Donc: ${LK}↖{→}(3;-3)$
De même, on a: $x_{{CB}↖{→}}=x_B-x_C=1-0=1$
Et on a: $y_{{CB}↖{→}}=y_B-y_C=0-1=-1$
Donc: ${CB}↖{→}(1;-1)$
4.
On constate que: $x_{{LK}↖{→}}=3x_{{CB}↖{→}}$ et $y_{{LK}↖{→}}=3y_{{CB}↖{→}}$
Par conséquent: ${LK}↖{→}=3{CB}↖{→}$.
Et donc: les vecteurs ${LK}↖{→}$ et ${CBF}↖{→}$ sont colinéaires.
Par conséquent, les droites (LK) et (CB) sont parallèles.