Les vecteurs

Exercice 9

On considère le plan muni du repère orthonormé $(O,{i}↖{→},{j}↖{→})$.
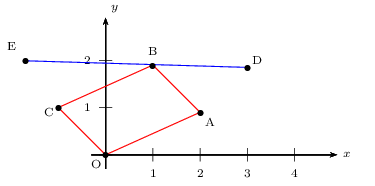
On considère les points A(2 ; 0,9), B(1 ; 1,9), C(-1 ; 1), D(4 ; 1,8), E(-1,7 ; 1,99).

1. Déterminer les coordonnées du vecteur ${AB}↖{→}$.
2. Déterminer la longueur AB.
3. Montrer que OABC est un paralléogramme.
4. On admet que ${EB}↖{→}(2,7\,;\,-0,09)$ et ${BD}↖{→}(3\,;\,-0,1)$
   Montrer que E, B et D sont alignés.
5. Montrer que B n'est pas le milieu du segment [ED].
6. Montrer que les droites (ED) et (AC) sont parallèles.
7. OABC est-il un losange?
Solution...

Corrigé




1. $x_{{AB}↖{→}}=x_B-x_A=1-2=-1$
   $y_{{AB}↖{→}}=y_B-y_A=1,9-0,9=1$
   Donc ${AB}↖{→}(-1;1)$ .


2. $AB=$$∥{AB}↖{→}∥$$=√ {(-1)^2+1^2}=√ {2}$.


3. On a: ${OC}↖{→}(-1;1)$.
   Or: ${AB}↖{→}(-1;1)$.
   Donc: ${OC}↖{→}={AB}↖{→}$
   Et par là, OABC est un paralléogramme.


4. On a: ${EB}↖{→}(2,7;-0,09)$ et ${BD}↖{→}(3;-0,1)$
   On calcule: $det({EB}↖{→},{BD}↖{→})=2,7 ×(-0,1)-3 ×(-0,09)=0$
   Donc les vecteurs ${EB}↖{→}$ et ${BD}↖{→}$ sont colinéaires.
   Donc les points E, B et D sont alignés.


5. On constate que les vecteurs ${EB}↖{→}$ et ${BD}↖{→}$ n'ont pas les mêmes coordonnées.
   Donc ils ne sont pas égaux.
   Donc B n'est pas le milieu du segment [ED].


6. On obtient: ${ED}↖{→}(5,7;-0,19)$ et ${AC}↖{→}(-3;0,1)$
   On calcule: $det({ED}↖{→},{AC}↖{→})=5,7 ×0,1-(-3) ×(-0,19)=0$
   Donc les vecteurs ${ED}↖{→}$ et ${AC}↖{→}$ sont colinéaires.
   Donc les droites (ED) et (AC) sont parallèles.


7. On a démontré que $AB=√ {2}≈1,4$.
   De même, on obtient: $OA={√ {481}}/{10}≈2,2$.
   Les côtés consécutifs OA et AB n'ont pas la même longueur.
   Donc OABC n'est pas un losange.

Réduire...