 Statistiques à deux variables quantitatives
Statistiques à deux variables quantitatives
Dans le cours qui suit, on se réfère toujours à une série statistique à deux variables quantitatives $(x_i;y_i)$ (pour $i$ allant de 1 à $n$, où $n$ est un entier naturel non nul).
I Indicateurs
Définition
Dans le plan muni d'un repère orthogonal, l'ensemble des points $M_i(x_i;y_i)$ représentant la série s'appelle le nuage de points de la série.
Définition
Si $x↖{−}$ est la moyenne des $x_i$, et $y↖{−}$ est la moyenne des $y_i$, alors le point $G(x↖{−}\,;\,y↖{−})$ s'appelle le point moyen de la série.
 Exemple
Exemple
On suit un groupe de 25 élèves de la première à la terminale. La série des $x_i$ donne leurs moyennes de maths en première. La série des $y_i$ donne leurs moyennes de maths en terminale. Les séries sont données ci-dessous.
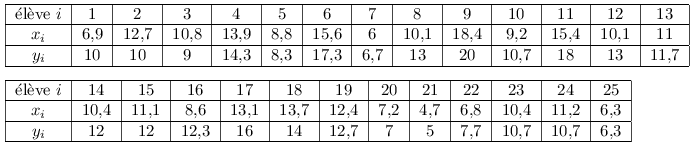
Représenter le nuage de points associé à la série double des $(x_i;y_i)$.
Soit $G(x↖{−}\,;\,y↖{−})$ le point moyen de la série. Placer G sur le dessin précédent.
Corrigé
Le nuage de points associé à la série double des $(x_i;y_i)$ est représenté ci-dessous.
On a: $x↖{−}={6,9+12,7+...+11,2+6,3}/{25}=10,592$
Et: $y↖{−}={10+10+...+10,7+3,3}/{25}=11,536$
Donc on obtient: $G(10,592\,;\,11,536)$.
G est le "centre de gravité" du nuage; il est dessiné en rouge sur le graphique.
Définition et propriété
La variance de la série des $x_i$ est le nombre
$V(x)={1}/{n}((x_1-x↖{−})^2+(x_2-x↖{−})^2+...+(x_n-x↖{−})^2)={1}/{n}(x_1^2+x_2^2+...+x_n^2)-x↖{−}^2$.
La variance permet de mesurer l'écart à la moyenne des valeurs d'une série statistique simple. Plus elle est grande, plus les valeurs sont dispersées par rapport à leur moyenne.
L'écart-type de la série des $x_i$ est le nombre
$ σ (x)=√ {V(x)}$.
Noter que la seconde formule donnant la variance génère potentiellement moins d'erreurs d'arrondis que la première car la moyenne (souvent approchée) n'intervient qu'une fois.
Définition
La covariance de la série des $(x_i;y_i)$ est le nombre
$\cov (x;y)={1}/{n}((x_1-x↖{−})×(y_1-y↖{−})+(x_2-x↖{−})×(y_2-y↖{−})+...+(x_n-x↖{−})×(y_n-y↖{−}))$.
La covariance permet de mesurer la dispersion des points du nuage par rapport au point moyen d'une série statistique double. Plus elle est grande, plus les points sont dispersés par rapport à leur point moyen.
Propriété
$\cov (x;y)={1}/{n}(x_1×y_1+x_2×y_2+...+x_n×y_n)-x↖{−}×y↖{−}$
Noter que cette seconde formule donnant la covariance génère potentiellement moins d'erreurs d'arrondis que la première car les moyennes (souvent approchées) n'interviennent qu'une fois.
 Exemple
Exemple
On reprend l'exemple précédent concernant les notes de 25 élèves.
Les calculs seront arrondis à 0,001 près.
Déterminer la variance de chacune des séries simples.
Déterminer la covariance de la série double.
Corrigé
On utilise la seconde formule pour chacun des calculs.
On a: $V(x)={1}/{25}(6,9^2+12,7^2+...+6,3^2)-x↖{−}^2={3072,78}/{25}-10,592^2≈10,721$
Donc: $V(x)≈10,721$
$V(y)={1}/{25}(10^2+10^2+...+6,3^2)-y↖{−}^2={3666,48}/{25}-11,536^2≈13,580$
Donc: $V(y)≈13,580$
$\cov (x;y)={1}/{25}(6,9×10+12,7×10+...+6,3×6,3)-x↖{−}×y↖{−}={3329,76}/{25}-10,592×11,536≈11,001$
Donc: $\cov (x;y)≈11,001$
Ces 3 valeurs se trouvent directement à l'aide de la calculatrice. Pour les Casio: mode "Statistiques, menu "Calculs", menu "Séries à 2 variables",.
Ne pas oublier de mettre tous les effectifs à 1 pour chacune des séries.
II Ajustements
Définition
Un ajustement est la détermination d’une courbe approchant au mieux un nuage de points dans le plan.
Un ajustement affine est la détermination d’une droite approchant au mieux un nuage de points dans le plan.
Propriété
Soit $Δ$ une droite ajustant le nuage de points.
Soient $d_1$, $d_2$, ..., $d_n$ les distances "verticales" entre les points $M_i$ et la droite $Δ$.
Il existe une droite unique telle que la somme $d_1^2+d_2^2+...+d_n^2$ soit minimale.
Cette droite constitue un ajustement affine du nuage par la méthode des moindres carrés.
Elle s'appelle droite de régression de $y$ en $x$.
Elle a pour coefficient directeur $a={\cov (x;y)}/{V(x)}$
Cette droite passe par le point moyen $G(x↖{−}\,;\,y↖{−})$.
 Exemple
Exemple
On reprend l'exemple précédent concernant les notes de 25 élèves.
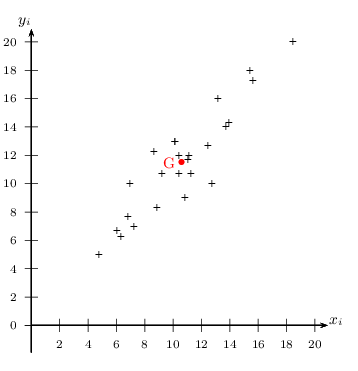
Déterminer l'équation $y=ax+b$ d'une droite d'ajustement du nuage par la méthode des moindres carrés, puis tracer cette droite sur le graphique.
$a$ sera arrondi à 0,001 près, et $b$ à 0,01 près.
Corrigé
La droite de régression de $y$ en $x$ admet une équation du type $y=ax+b$.
Elle pour coefficient directeur $a={\cov (x;y)}/{V(x)}≈{11,001}/{10,721}≈1,026$
De plus, elle passe par le point moyen $G(10,592\,;\,11,536)$.
Donc on a: $11,536≈1,026×10,592+b$
Et par là: $11,536-1,026×10,592≈b$
Soit: $b≈0,67$
En résumé: $a≈1,026$ et $b≈0,67$
Ces 2 valeurs se trouvent directement à l'aide de la calculatrice. Pour les Casio: mode "Statistiques", menu "Calculs", menu "Regression", puis menu "aX+b".
La droite d'ajustement du nuage par la méthode des moindres carrés (droite de régression de $y$ en $x$) est représenté ci-dessous.
Elle passe par G et a pour ordonnée à l'origine $b≈0,67$.
Définition
Le coefficient de corrélation linéaire est le nombre
$r={\cov (x;y)}/{σ (x) × σ (y)}$.
Propriété
Le coefficient de corrélation linéaire $r$ est compris entre $-1$ et $1$
$-1≤ r ≤1$
Plus $r$ est proche de 1 ou de $-1$, plus la corrélation est forte, et meilleur est l'ajustement affine.
$r$ a le même signe que $a$ (pente de la droite de régression de $y$ en $x$).

Propriétés
Le coefficient de corrélation n’est pas sensible aux unités de chacune des variables.
Le coefficient de corrélation est extrêmement sensible aux valeurs extrêmes.
On considère que si $|r|>0,9$, alors l'ajustement permet des prévisions convenables.
Mais l'interprétation d'un coefficient de corrélation dépend du contexte.
Une corrélation de 0,9 peut être très faible si l'on vérifie une loi physique en utilisant des instruments de qualité.
Une corrélation supérieure à 0,5 peut être suffisante dans les sciences sociales où il est difficile de prendre en compte tous les paramètres.
 Exemple
Exemple
On reprend l'exemple précédent concernant les notes de 25 élèves.
Les calculs seront arrondis à 0,01 près.
Déterminer le coefficient de corrélation linéaire $r$ de la série double. Un ajustement affine est-il justifié?
Un élève a 10 de moyenne en première. Quelle moyenne peut-il espérer avoir en terminale?
Corrigé
$r={\cov (x;y)}/{σ (x) × σ (y)}={\cov (x;y)}/{√ {V(x)} × √ {V(y)}}≈{11,001}/{√ {10,721} × √ {13,580}}≈0,91$.
Cette valeur se trouve directement à l'aide de la calculatrice.
On a $|r|>0,9$. Par conséquent, un ajustement affine se justifie.
On calcule $10a+b≈10×1,026+0,67≈10,9$
Un élève ayant 10 de moyenne en première peut espérer avoir environ 11 de moyenne en terminale.
Propriété
Dans le cas où un ajustement par une courbe semble justifié, on tente, par un changement de variable, de se ramener à un ajustement affine.
La méthode est explicitée dans l'exemple qui suit...
 Exemple
Exemple
Un biologiste étudie la croissance d'une culture bactérienne en fonction du temps.
Au départ de l'expérience, la densité bactérienne est de $10\,000$ bactéries par millilitre.
Le biologiste mesure la densité bactérienne à divers instants $t_i$ ( en heures )et obtient le tableau suivant:

Le nuage de points associé à la série ($t_i,y_i$) est représenté ci-dessous.
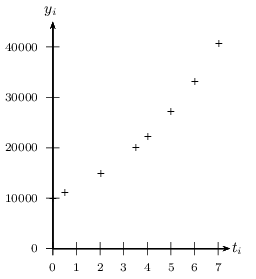
1. La forme du nuage suggère qu'un ajustement est concevable. Le biologiste écarte un ajustement affine.
Pour quelle raison ?
2. Le biologiste, très inspiré, choisit une nouvelle variable $z_i=\ln y_i$, et il construit le tableau suivant ( dans lequel il arrondit les valeurs des $z_i$ au millième )

Que vaut $z_8$ ?
3. Le nuage de points associé à la série ($t_i,z_i$) est représenté ci-dessous.
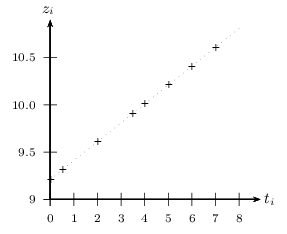
Déterminer à l'aide de votre calculatrice une équation de la droite de régression de $z$ en $t$.
4.
La droite est tracée ci-dessous.
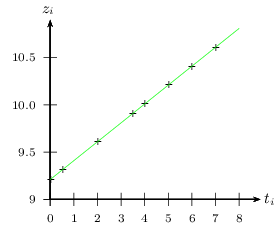
L'ajustement est très satisfaisant. Pourquoi?
5.
Heureux, le biologiste en déduit alors une formule permettant d'estimer la densité bactérienne $y$ en fonction du temps $t$.
Déterminer cette formule.
6. Estimer par le calcul la densité bactérienne (arrondie à la centaine) au bout de 6 heures et trente minutes.
Solution...Corrigé
1. Le biologiste écarte un ajustement affine car les points ne se distribuent pas autour d'une droite.
2. $z_8=\ln 40\,000≈10,612$
3. A l'aide de la calculatrice, on trouve que la droite de régression de $z$ en $t$ a pour équation: $z=at+b$, avec $a≈0,200$ et $b≈9,21$
4. A l'aide de la calculatrice, on trouve que le coefficient de corrélation linéaire $r$ de la série double vérifie: $r≈1$. C'est quasi parfait! On a largement $|r|>0,9$. L'ajustement est donc très satisfaisant.
5. On a alors: $z=0,2t+9,2103$ et $z=\ln y$
Donc: $\ln y=0,2t+9,2103$
Et par là: $y=e^{0,2t+9,2103}$
6. 6h30 donnent $t=6,5$, et donc: $y=e^{0,2×6,5+9,2103}≈36\,691$
On peut estimer que la densité bactérienne au bout de 6 heures et trente minutes est d'environ $36\,700$ bactéries par millilitre.