Lois à densité
Lois à densité
A SAVOIR: le cours sur la densité
Exercice 1
- Robin tire une flèche sur une cible en forme de disque de rayon 1 mètre.
Sa flèche atteint la cible à coup sûr.
Soit X la variable aléatoire donnant la distance (en mètres) entre le point d'impact de la flèche et le centre O de la cible.
X admet pour densité la fonction $f(x)=ax$ sur $[0;1]$.
Déterminer la valeur de $a$. - a. Quelle est la probabilité que la flèche de Robin soit à moins de 10 cm du centre.
b. Quelle est la probabilité que la flèche de Robin soit entre 10 et 20 cm du centre.
c. On admet que $E(X)={2}/{3}$.
Interprétez cette valeur de deux façons différentes.
Corrigé
- La densité $f$ est linéaire et est définie sur [0;1]. Sa représentation graphique est donc un segment de droite passant par l'origine.
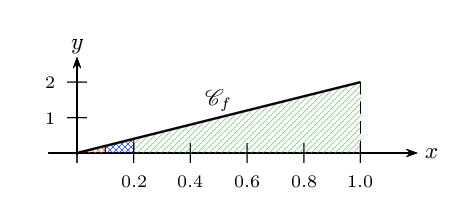
Comme $f$ est une densité, l'aire du domaine situé entre $C_f$ et l'axe des abscisses vaut 1.
Or, le domaine en question un triangle de base $1-0=1$ et de hauteur $f(1)=a×1=a$.
C'est le "grand" triangle hachuré en vert qui touche l'origine.
Son aire vaut donc: ${1×a}/{2}=0,5a$.
On obtient donc $0,5a=1$. Et par là: $a=2$. Donc finalement, $f(x)=2x$. -
a. La probabilité cherché est: $$p(0≤X≤0,1)=∫_0^{0,1} f(x)dx$$.
Or, le domaine dont on cherche l'aire est un triangle rectangle de base $0,1-0=0,1$ et de hauteur $f(0,1)=2×0,1=0,2$.
C'est le "petit" triangle hachuré en rouge et vert qui touche l'origine.
Donc: $$p(0≤X≤0,1)={0,1×0,2}/{2}=0,01$$
b. La probabilité cherché est: $$p(0,1≤X≤0,2)=∫_{0,1}^{0,2} f(x)dx$$.
Or, le domaine dont on cherche l'aire est un trapèze de bases $f(0,1)=0,2$ et $f(0,2)=0,4$ et de hauteur $0,2-0,1=0,1$.
C'est le "petit" trapèze hachuré en bleu et vert.
Donc: $$p(0,1≤X≤0,2)={0,2+0,4}/{2}×0,1=0,03$$
c. Première interprétation.
On a: ${2}/{3}≈0,67$
Sur un très grand nombre de lancers, Robin tire en moyenne à environ 67 cm du centre de la cible.
Il n'est pas très doué...
Seconde interprétation.
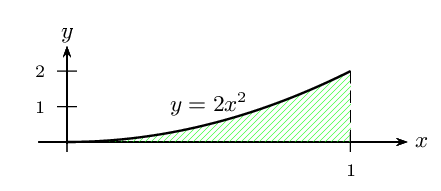
On a: $$E(X)=∫_0^{1} x.f(x)dx=∫_0^{1} 2x^2 dx$$.
Le trinôme du second degré $2x^2$ est continu et positif.
Donc $E(X)$ représente l'aire du domaine situé entre la parabole représentant le trinôme, l'axe des abscisses, et la droite d'équation $x=1$.
Ce domaine (hachuré en vert ci-dessous) a donc une aire égale à ${2}/{3}$ d'unités d'aires.